The saturation control of pretty much all image processing software is an unfortunate misnomer, to say the least. It actually controls either the chroma in Ych-like spaces (computed from CIE Yxy 1931, Yuv or YCbCr spaces), or some remote idea of saturation as used by HSL spaces, which are essentially a polar rewriting of RGB coordinates (usually expressed in sRGB space).
The “saturation” as defined by the HSL space has been proven times and times again to hold no perceptual meaning and finds its origin into the first GUI of limited computers doing integer arithmetic. We can show here another illustration as to why HSL/HSV are meaningless to computer graphics. The following gradients where generated at constant CIE 1931 luminance $Y = 0.4075$ and at constant chroma. For each color model, the chroma has been empirically adjusted to the maximum value that produces a gradient fully contained within sRGB gamut (without clipping). For the HSL/HSV models, since luminance and chroma are not defined, S and L/V have been roughly adjusted visually to match the perceptual gradients.










It is immediately noticeable that HSL and HSV do not degrade at constant lightness, nor provide constant chroma or “saturation”. Also, the green range spans too wide on the gradient, compared to other hues, while yellow only has a thin line, and cyan is also compressed. The perceptual hue gradients display no yellow, because yellow is only found at higher luminances and should not appear here. HSL/HSV should display olive-green and light brown in place of yellow, that is, “dark yellow”.
The model parameters used are :
- HSL : $S = 0.5$, $V = 0.7$,
- HSV : $S = 0.4$, $L = 0.9$,
- CIE Lab 19761 : $L = 70 / 100$, $c = 38 / 100$,
- IPT 20132 : $I = 0.676$, $c = 0.22$,
- JzAzBz 20173 : $Jz = 0.01022$, $c = 0.48$,
- Oklab 2020-20214 : $I = 0.7438$, $c = 0.12$
- darktable UCS 22 (developed below) : $L = 0.71$, $c = 0.36$
- Yrg 20195 : $Y = 0.4311$, $c = 0.085$.
It is worth noting that Kirk Yrg 2019 is a scene-linear (radiometrically-scaled) space designed for color-grading. The Ych/Yrg rewriting is meant to have an uniform hue repartition around the white point, but has been designed for the sole purpose of having well-scaled GUI controls directly translatable into RGB parameters for algorithms running in scene-referred RGB. It uses the CIE 2006 definition of Y, such that $Y_{CIE \, 1931} = 0.9453 Y_{CIE \, 2006}$.5 It is therefore a kind of Yuv space, while CIE Lab, JzAzBz, IPT and Oklab are perceptually-uniform (non-radiometrically-scaled) spaces.
#What is saturation anyway ?
Saturation is a word that has been abused by decades of bad computer graphics, mixing its scientific meaning with its common usage. It is useful here to reboot the CIE definitions:
CHROMA: colourfulness of an area judged as a proportion of the brightness of a similarly illuminated area that appears grey, white or highly transmitting.6
SATURATION: colourfulness of an area judged in proportion to its brightness.7
BRIGHTNESS : attribute of a visual perception according to which an area appears to emit, transmit or reflect, more or less light. 8
COLORFULNESS : attribute of a visual perception according to which the perceived colour of an area appears to be more or less chromatic. 9
So, if we untangle this we get that:
- chroma is relative to the grey colour having the same brightness,
- saturation is relative to its own brightness.
This yields two different representations of colour :
- a Lightness, Chroma, Hue system,
- a Brightness, Saturation, Hue system.
An useful, graphical, translation between both systems can be found on David Briggs’s website10, we reproduce it here :

Translated into computer graphics terms, the lightness is a perceptual rescaling of the radiometric luminance (CIE Y component). For this scaling, Oklab uses a simple cubic root, CIE Lab 1976 uses a cubic root with a noise threshold, and other models may use the Dolby Perceptual Quantizer (JzAzBz) or a Michaelis-Menten analog, but the principle of a simple cubic root holds : it raises mid-tones and connects smoothly with medium black and white which it leaves unchanged. The lightness axis goes through the grey gradient. The chroma is orthogonal to the lightness. All colours share the same lightness axis.
Saturation, however, is not an unique axis. Each colour has its equi-saturation axis going through it from the black point. Conversely, the equi-brightness axis is also a propriety of each color, oriented in a parallel direction to the white → primary color.
An important consequence is that desaturating should turn red into pink then into white. This is consistent to what happens when diluting pigments into white paint, or mixing a colored light with white light, if we forget the Abney effect.
This is not what computer graphics “saturation” algorithms do. Below are the sRGB gamut slices at constant hue, for the hues of the Rec709 primaries, from my previous post, the sRGB book of color (top line). See what happens to them when we reduce their chroma by 50% in Kirk Yrg (middle line) and then by 75% (bottom line) :









This effectively degrades colours into a monochrome image where the grey shade is defined by the original luminance of the pixel, because we use an Yuv kind of space. Of course, “desaturation” based on HSL, HSV, or RGB averaging will have another effect, but it should be fairly close visually.
Problem is, outside of computer graphics, the result of a desaturation is expected to be a paler colour. That is less colourful and lighter. Effectively, this falls back to turning saturated colours into their pastel equivalents, and pastel colours into their primary equivalent. This cannot be done with the typical chroma-based “desaturation”, but needs a real saturation change, as defined by the CIE.
As a side-note, film emulsions can perfectly degrade saturated colors to light, pastel colors by a bleaching effect. It is about time that the digital world catches up on film to suppress this insane film nostalgia based on an alleged intrinsic property of film while the truth is film sensitometry was carefully crafted by people who conducted extensive colour research before.
#Choosing a colour space
Chroma is a perceptual dimension of colour, but it can still be dealt with either in radiometrically-scaled spaces (Yuv, Ych) or in perceptually-uniform spaces (Lab, Lch). However, brightness is linked to both lightness and chroma, and for proper scaling of the effect along both directions, a perceptually uniform color space is the obvious choice. However, we need to stop and discuss what perceptually uniform means, because it is casted like a magic spell by too many software developers.
Colour spaces like CIE Lab 1976, IPT, JzAzBz etc. aim at having euclidean distances uniformly spaced. Euclidean distances measure the delta E, that is the perceptual difference between 2 colors, in order to control, predict and possibly reduce the colour dissimilarity between a reference and a test image or a reference and a test colour. Such spaces are not designed to modify colour but to provide a metrology framework in which a simple 3D euclidean distance has a cognitive meaning.
Colour spaces like CIECAM 02 and 16, Hunt and Nayatani, aim at being colour adaptation models, meaning they describe the appearance of colours with respect to the viewing conditions (illuminant colour, surround lighting, etc.) and provide models to adapt the colours, that is to retain the same appearance while the viewing conditions change. But here, Hunt and CIECAM models where designed for image reproduction (that is, reflective surfaces) while Nayatani was designed for lighting engineering (that is, emissive objects).
Not many models are aimed at allowing colour manipulation in a perceptually-defined way. Such models exhibit an even hue repartition over the chromaticity diagram, as well as straight equi-hue lines (unlike Abney lines) and circular equi-chroma. But when we take into account the limitations of colour adaptation models (bounded white luminance, viewing conditions, etc.), the choice gets scarce.
There are several perceptually uniform colour spaces that explicitly include the support of saturation and brightness based on observer data :
- the Hunt model, built between 1952 and 1995 by a Kodak researcher, Robert William Gainer Hunt,
- the Nayatani et al. model, built 1981 and 1995,
- the CIECAM02 and its second version, CIECAM16.
But they have several problems :
- the Hunt model is not invertible, so while we would be able to compute the saturation and let the user change it, we would be unable to bring back the result into the RGB realm,
- The Nayatani model is complicated, using many transcendent functions sequentially (log and power),
- CIECAM16 has a numerically unstable behaviour, with a crooked gamut shape,
- All of them rely on bounded luminance, unsuitable for HDR signals.
The colour space review coming with the designing of Oklab4 is useful to visualize the fitness of colour manipulation by looking at the shape of the visible gamut and the repartition of Munsell hues (graphs taken from Ottosson):

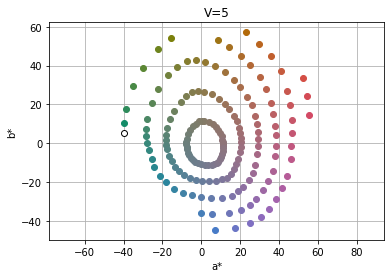


The spaces exhibiting a circular repartition of chroma are the best suited for this work, that is Oklab and CIECAM16. Indeed, if we are to digitally rotate hues around white, the rotated colours will not end up at the same perceived chroma as the original colours in spaces that have ellipsoidal chroma rings. Conversely, applying digitally a chroma gain may not hit all the hues with same visual intensity if the chroma rings are not circular.
However, a look at the gamut shows that CIE CAM 16 has a highly non-convex boundary that will cause problems when pushing colors :

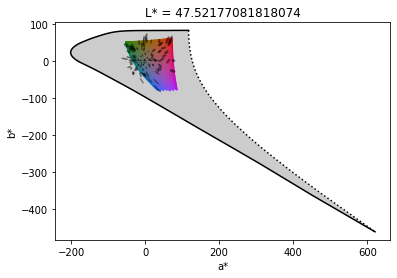


This means we will use Oklab as a starting point. It is almost as good as CIE CAM16 as far as Munsell hues go, but more simple. But since it is a Lightness/Chroma space, we will need to rewrite it as a Brightness/Saturation space and we need to assert how the constant hue planes behave. For this, we project Munsell colours on the $(L, c)$ plane in Oklab and look for the geometry of the predictions :
We plot the lines of equal lightness and equal chroma in Munsell notation system. The hues are given in the title in Munsell notation as well as in Oklab hue angle, as (average ± standard deviation) radians in $[0; 2 \pi]$. Since angles cannot be averaged directly (because $0 \equiv 2 \pi$), the Lch hue angles are converted to complex unit vectors, and the vector coordinates are averaged in the complex plane. The average angle is taken as the argument of the average complex vector, and the standard deviation is directly on the complex coordinates.
If Oklab was perfect, the mesh formed by those lines would be a perfect square grid, with orthogonal lines oriented in the same direction as the main axes. We can see that Oklab does a fairly good job at predicting Munsell values and chromas, however, the yellow-green region is really crooked in the extreme chromas. Also, the yellow region has equi-lightness lines slightly dropped, while the opposite region, purple, is has the equi-lightness lines slightly raised.
What is a bit concerning, though, is the density of the mesh is not uniform across hues. The 10PB plate (purple-blue) hat 34 Munsell chroma units spanning over 0.35 Oklab chroma units, while the 10B plate (blue) has 18 Munsell chroma units spanning over 0.32 Oklab chroma units.
#Rewriting Oklab as Brightness-Saturation system
Oklab has the desirable property of leaving the gamut of RGB spaces shaped as a straight cone, while the hue slices of sRGB in JzAzBz showed above clearly demonstrate non-linearity at the boundary of the gamut:



The non-continuity of the blue primary slice is slightly concerning, we will have to assess later if it is a problem. Nevertheless, we can build a look-up table (LUT) of the gamut boundary as a simple linear hue-wise function, in the $(L, c)$ plane.
#Building the gamut LUT
The lower bound of the gamut is a straight line having constant saturation, that is a constant $s = \dfrac{c}{L}$ ratio. We create an RGB cube of 92×92×92 elements between $0$ and $1$, convert RGB coordinates to Oklab (L, a, b) then to Lch. The LUT is 2×1D and will store the $\arg \max(c)$ and $\arg \max(c / L)$ for each hue. A hue resolution of 1° is enough for the LUT. Then we apply anti-aliasing using a 5-taps 1D box blur.
The maximum chroma and saturation will allow us to compute the slope of the gamut boundary and the cusp for each hue. This is a reasonably fast operation to compute on-the-fly, and LUTs can be pre-computed for usual colour spaces.
#Parametrisation of the transform
Let $A$ denote the original colour in the $(L, c)$ plane of constant hue. $A$ has a saturation defined either as a ratio $s = \dfrac{c}{L}$ or as an angle $\gamma_1 = \arctan(s)$.
The user will be asked to define the saturation change by a proportional factor applied on the angle $\gamma_1$. This will define a rotation of the vector $\vec{S}$ around the black point to give the vector $\vec{S’}$, such that $||\vec{S’}|| = ||\vec{S}|| = \sqrt{L^2 + c^2}$ and $\arg(\vec{S’}) = k_1 \arg(\vec{S}) = k_1 \gamma_1 = \kappa \in [\alpha_1; \frac{\pi}{2}]$.
The fact that we know the limit of the gamut boundary and that we apply a transform which nicely falls back to a rotation of this boundary means that we can have built-in gamut sanitization, and saturation clipping yields a graceful gamut clipping that preserves gradients of lightness and chroma at constant hue.
Once the vector $\vec{S}$ has been rotated by an angle $\kappa - \gamma_1$, we need to rescale it to reach the line of equi-brightness. This reaches the new colour $A’’$ ported by the vector $\vec{S’’}$. The user will then be asked to define a brightness change that will proportionally scale the modulus of $\vec{S’’}$.
The equi-brightness lines are all parallel to the white → gamut cusp line, forming an angle $\delta$ with the horizontal. From the maximum saturation and chroma, we can compute the $(L, c)$ coordinates of the cusp :
$$ \begin{align} c_{cusp} &= \arg,\max(c)_h\\ L_{cusp} &= \dfrac{c_{cusp}}{\arg \max(s)_h}\\ \end{align} $$
Oklab can be scaled4. This means that, in HDR settings, when the white point exceeds 100 Cd/m², it suffices to normalize the XYZ coordinates by the Y of the white, then to convert to Oklab. White can thus be expected at 100%, which makes it easy to compute the slope of the equi-brightness line:
$$ \delta = \arctan\left(\dfrac{1 - L_{cusp}}{c_{cusp}}\right) $$
We now get a triangle $A A’’ O$ where $O$ denotes the origin of the axes and the black point. By the property of internal alternate angles between 2 parallel lines, $\gamma_1 = \gamma_2$ and $\widehat{A’’ A O} = \gamma_1 + \delta$.
Since the $A A’’ O$ triangle is scalene, we will have to resort to the law of sines :
$$ \dfrac{\sin(\delta + \gamma_1)}{||\vec{S’’}||} = \dfrac{\sin(\kappa - \gamma_1)}{||\vec{AA’’}||} = \dfrac{\sin(\pi - (\delta + \gamma_1) - (\kappa -\gamma_1))}{||\vec{S}||} $$
From which we deduce:
$$ ||\vec{S’’}|| = ||\vec{S}|| \dfrac{\sin(\delta + \gamma_1)}{\sin(\pi - \delta - \kappa)} $$
On this vector, the brightness scaling can be applied from the user parameter : $||\vec{S’’’}|| = k_2 × ||\vec{S’’}||$.
Converting back to Lch is easy:
$$ \begin{align} \kappa &= k_1 × \gamma_1 \in [\arg \max(s)_h; \pi / 2]\\ L &= ||\vec{S’’’}|| \sin(\kappa)\\ c &= ||\vec{S’’’}|| \cos(\kappa)\\ \end{align} $$
where the angle $\kappa$ is clipped to fit in the gamut by $[\arg \max(s)_h; \pi / 2]$.
#Results
#Synthetic
The experiments are done in darktable, using unbounded RGB on the 8 bits PNG files from the post sRGB book of color. The working gamut is Rec2020 and so the gamut boundary as well as the equi-brightness lines are computed against it. The upper gamut cone is not sanitized. The file is then encoded back to sRGB.



























The bottom cone holds well even for insane saturation increases that are guaranteed to exceed the sRGB gamut. On the other hand, the upper cone clips at non-constant hue for heavy desaturation, which may be explained by the fact that the sRGB gamut has a curved upper cone while the desaturation moves in a rectilinear direction. This should be handled when converting back to bounded RGB.
One issue we observe here is how yellow degrade to a muddy variant as saturation rises, while we would expect it to degrade to something close to cadmium yellow, in the spirit. It may be consistent with the oddities displayed in the mesh of Munsell colours for the 10Y (yellow) plate, where the extreme chroma values are not only compressed, compared to the greyer shades, but also the lines of equi-lightness are slanted.
#Natural
The next result comes from a picture made myself in studio, under high-CRI D55 lighting with a profiled camera. The starting material is the already-edited JPEG. We use the color balance RGB module from darktable to shift saturation in Oklab and apply the same settings on chroma in Kirk Yrg :





The saturation approach allows effectively to bleach the highlights to get the beloved desaturation coming with most film emulsions, while increasing the density of colours in shadows. The result reinforces both the colour and the lightness contrast. This effect is customarily obtained by applying a channel-wise sigmoidal contrast-increasing curve in RGB, with two major drawbacks : the hue is not preserved through a channel-wise non-linear operator, and the (de)saturation is a by-product of the contrast increase and not an orthogonal, individual parameter. As the amount of desaturation cannot be separated from the amount of contrast increase, and the resulting desaturation cannot be correlated to any perceptual color property, the result is unpredictable and that makes for a very bad, random, workflow.
The chroma approach, working at constant luminance, makes the shadows degrade to fluorescent colours and yields a less natural result.
#Choosing the gamut
I want to be very clear on the fact that all we have done so far is to change the direction in which the saturation/desaturation pushes colours. This is geometric hocus-pocus and has nothing to do with perception, it does not take into account the greyness boundary (linked to Evans & Swenholt’s notion of fluorence11) nor the Helmholtz-Kohlrausch effect. Yet it already yields more pleasing results than the pure chroma approach and meets the pastel design goal, which is already a success for such a simple trigonometric trick.
The gamut against which we computed the equi-brightness direction has been set to darktable’s default working RGB space : Rec2020 (linear). Using Rec709 makes the effect stronger and the gamut clip at lower saturation values. In any case, it would be interesting to evaluate if we can use directions independent from the RGB working space, but linked to human vision. That is, fitting the $\delta(hue)$ angle to some perceptual reality and make it independent from the RGB spaces heuristics.
#Building a new perceptual color space for color correction
After trying to fix Oklab for a dozen of hours, it appeared that the numerical issues it raises are grounded into design constraints we don’t need for the current task. And so do most of the other perceptual spaces.
First of all, Oklab is a retro-fit of CIE CAM16 using a simpler model, using CIE CAM16 predictions as a training set, and trying to approximate them by a model retaining the algorithmic simplicity of CIE Lab. It will therefore inherit the flaws from both approaches.
These perceptual spaces are designed to either compute a delta E or to adapt the appearance of an image as the viewing conditions change, that is retain the perception and translate it into a different viewing context. For this, they rely on an opponent color space : a/b or P/T depending on models. To go this opponent space, they convert to cone response space (LMS), then apply a non-linear transform in 3D. Because this non-linear transform relies on an additive light model and usually does not tolerate negative input (CIE Lab as Oklab use a cubic root), the cone response space has to be fitted with two unsolvable constraints :
- being hue-linear,
- yielding positive cone intensities for all visible colors.
The numerical trade-offs this creates are very damaging for both the physiological accuracy of the model and the numerical accuracy of the fitting to experimental datasets.
Also, this 3D mapping is tilting the perceptual lightness plane, as we saw above for Oklab. In any case, none of them accounts for brightness including the compensation for Helmholtz-Kohlrausch effect.
If we review the need for an opponent space for our application here, we see that it is merely used to compute the chroma (as a metric of the distance to achromatic) as $c = \sqrt{a^2 + b^2}$ and the hue as $h = \arctan(b / a)$. While we need an uniform delta E over the perceptual space, we don’t need to compute or express it. Fortunately, the Munsell dataset provides us directly with hues and chromas, and does not bother with opponents colour dimensions because artists don’t ever need them.
We want a proper scaling of perceptual correlates like brightness and saturation for the colour change effect to be evenly scaled over the visible range.
So we could fit an Lch model directly from Munsell hue-value-chroma dataset, without going through LMS space and without even tilting the lightness plane. Doing so, we will not try to model the physiology of vision, but approach the problem as a geometric space distortion where the Munsell hues and the saturations (as a ratio of chromas / values) can be predicted by a 1D mapping from the hues, chromas and lightnesses of forming the principal dimensions of the model.
This model will need to be invertible. We will try to fit brightness data to derivate correlates of perceptual brightness accounting for the Helmholtz-Kohlrausch effect. Using the brightness and saturation correlates, we will rewrite our image saturation algorithm in terms of perceptually-even operators.
#Fitting Munsell Value with lightness
#Lightness model
Various models have been proposed over the years to fit the lightness correlate from Y luminance, and many different equations can be fitted with very good accuracy on the data because the range is quite small. I propose a generalized Michaelis-Menten equation, as used in IPT and CIE CAM97, 02 and 16 do, because of its link with cone response.12
It is worth mentioning, though, that the Y luminance is not directly a cone response and CIE CAM 97 to 16 use an achromatic $A$ stimulus here, derivated from a linear combination of the physiological cone response. In other words, there is more to lightness than just CIE Y luminance, and we choose here to ignore that fact for the sake of hue-linearity and to avoid going through an intermediate LMS space.
We form the a-priori model:
$$L^* = V_{Munsell} = a \dfrac{Y^c}{b^c + Y^c}$$
The choice of $a$ is critical for the invertibility properties as it defines the upper lightness bound (saturation level) of the model. Indeed, the inverse model yields:
$$Y = \left(\dfrac{b^c L^*}{a - L^*}\right)^{1 / c}$$
where it becomes obvious that the lightness model will be valid only for lightness levels verifying $a - L^* > 0$. The saturation level is to be chosen carefully as it is the practical bound of the model. We know that the static dynamic range of the human retina cone cells is expected around 6 EV12. However, the adaptation to luminosity is a local and temporal scheme13 where the $b^c$ half-saturation parameter is adapted dynamically through time and space, such that the resulting dynamic range can be quadrupled. This is more likely the result of pupil dilatation, that acts like a physiological exposure bracketing and it will be very difficult to include in a colour appearance model, so I need to discard it.
CIE CAM1614 uses the cone adaptation equation :
$$f(x) = sign(x)\frac{400(F_L |x| / 100)^{0.42}}{27.13 + (F_L|x| / 100)^{0.42}} + 0.1$$
From which we can deduce that $b^c / a = 27.13 / 400$ and $b / a = 27.13^{1 / 0.42} / 400 = 6.47$. I will therefore constrain the $b/a$ ratio to 6.5 while refitting the equation for $(a, c)$. This yields :
$$L^* = V_{Munsell} = 2.64385176 \dfrac{Y^{0.57145904}}{1.67207394022 + Y^{0.57145904}}\label{L-eqn}$$
The reverse model yields :
$$Y = \left(1.67207394022 \dfrac{L^*}{2.64385176 - L^*}\right)^\frac{1}{0.57145904}$$
Which clearly shows that it is defined for $L^* < 2.645$. In practice, a lightness $L^*$ of 2.64 maps to a relative luminance $Y_r = 145852$, that is 145852 times brighter than perfect diffuse white or 12 EV above, so the lightness bound should not be an issue for practical use.
#Comparison with CIE CAM16
A paper yet to be published15, by Hellwig and Fairchild, aims at simplifying the CIE CAM16 correlates by reviewing their interdependency and assumptions. The simplified achromatic response becomes :14
$$A = 2 R_a’ + G_a’ + 0.05 B_a’ - 0.305$$
$$f(x) = sign(x)\frac{400(F_L |x| / 100)^{0.42}}{27.13 + (F_L|x| / 100)^{0.42}} + 0.1$$
It is noted that the function, however, is unstable near zero.14 It also never reaches zero, which would be a problem for color-grading applications, since the black end of the working RGB spaces gamut could be assigned a non-zero saturation, resulting most likely in out-of-gamut code values.
$R’$, $G’$, $B’$ are the linear cone responses in Hunt-Pointer-Estevez cone space obtained from CIE XYZ 1931 coordinates by a matrix dot product :
$$ \begin{bmatrix} R’ \\ G’ \\ B’ \\ \end{bmatrix} = \begin{bmatrix} 0.38971 & 0.68898 & -0.07868 \\ -0.22981 & 1.18340 & 0.04641 \\ 0.00000 & 0.00000 & 1.00000 \\ \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix} $$
$X_c$, $Y_c$ and $Z_c$ are the adapted CIE XYZ 1931 coordinates for the CIE E illuminant, which is defined as the equi-energy illuminant ($X = Y = Z$ or $x = y = 1/3$ in CIE xyY 1931 space).
The darktable UCS is already non-linearily adapted but only on the CIE Y 1931 component. We can here compare both transfer functions, with the CIE CAM16 cone adaptation function normalized by 140 to reach 1 in 1 :
$R_a’$, $G_a’$ and $B_a’$ are the non-linear cone responses, adapted from the $R’$, $G’$, $B’$ using the generalized Michaelis-Menten function:14
$$f(x) = sign(x)\frac{400(F_L |x| / 100)^{0.42}}{27.13 + (F_L |x| / 100)^{0.42}} + 0.1$$
It is noted that the function, however, is unstable near zero.14 It also never reaches zero, which would be a problem for color-grading applications, since the black end of the working RGB spaces gamut could be assigned a non-zero saturation, resulting most likely in out-of-gamut code values.
$R’$, $G’$, $B’$ are the linear cone responses in Hunt-Pointer-Estevez cone space obtained from CIE XYZ 1931 coordinates by a matrix dot product :
$$ \begin{bmatrix} R’ \\ G’ \\ B’ \end{bmatrix} = \begin{bmatrix} 0.38971 & 0.68898 & -0.07868 \\ -0.22981 & 1.18340 & 0.04641 \\ 0.00000 & 0.00000 & 1.00000 \end{bmatrix} \begin{bmatrix} X_c \\ Y_c \\ Z_c \end{bmatrix} $$
$X_c$, $Y_c$ and $Z_c$ are the adapted CIE XYZ 1931 coordinates for the CIE E illuminant, which is defined as the equi-energy illuminant ($X = Y = Z$ or $x = y = 1/3$ in CIE xyY 1931 space).
The darktable UCS is already non-linearily adapted but only on the CIE Y 1931 component. We can here compare both transfer functions, with the CIE CAM16 cone adaptation function normalized by 140 to reach roughly 1 in 1 :
To see how the darktable UCS L correlates with CIE CAM16 A achromatic response, we create a synthetic LUT of $(X, Y, Z)$ triplets in CIE XYZ 1931 2° under CIE E illuminant and project them into both spaces :
The well-known negatives created by the Hunt-Pointer-Estevez cone transform matrix appear clearly here. They make absolutely no sense from a physiological point of view: positive light stimuli are not expected to create negative perceptions. Apart from the scaling difference (I have not found the reason why CIE CAM 97 to 16 map perfect diffuse white to 400…) the curves are fairly correlated for positive values, with a larger error in low lights. Since it is difficult to infer a valid achromatic response where CIE CAM16 A yields negatives, no further attempt will be made to fit more closely the dt UCS L* on CIE CAM 16 achromatic response, but it would be numerically feasible, since the R² is 0.84.
#Fitting chromaticity
#Data
We use Munsell Renotation data from 194316, taken from the datasets of the Python computational library Colour Science 0.3.16 . We adapt them to the CIE E illuminant, equi-energy ($X = Y = Z$) through the CIE CAT16 transform, because it will prove to be the less challengin to fit. It is also the method used in CIE CAM1614.
Projecting it onto the CIE xyY 1931 chromaticity plane shows the whole problem : there is no immediate correlation between perceptual properties of colour (hue and chroma) and their radiometric coordinates in normalized cone space. That is to say that colour is not merely a product of our retina.
The initial colour correlates are quite bad :
When projecting onto the orthogonal axis, the issue is essentially the same :

The chroma and the luminance spacing are not properly scaled compared to each other, and the perceptual chroma is exaggerated at lower luminances, compared to the same chroma at higher luminance.
#Objective
A perceptual space means that each of the 40 Munsell hue should have an angle of $\frac{2\pi}{40}$ with the next and each chroma should occupy a circle centred around white and separated by a radius from the next circle :
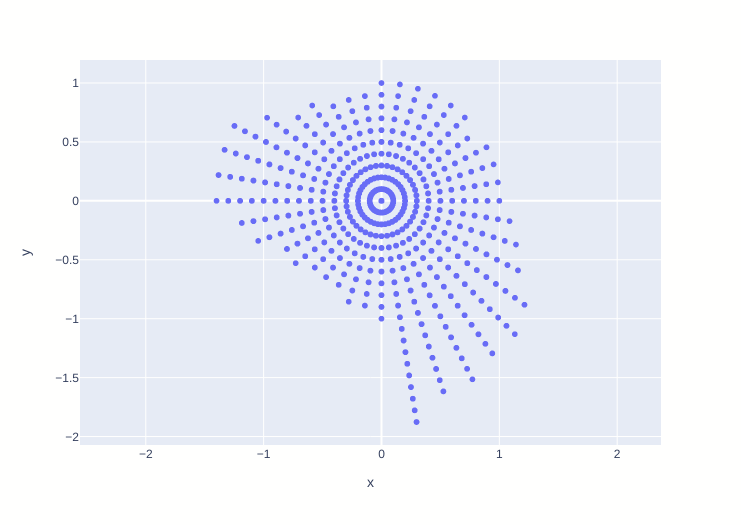
Similarly, the orthogonal plane should display a perfect rectangular mesh for the equi-chroma and equi-lightness lines :
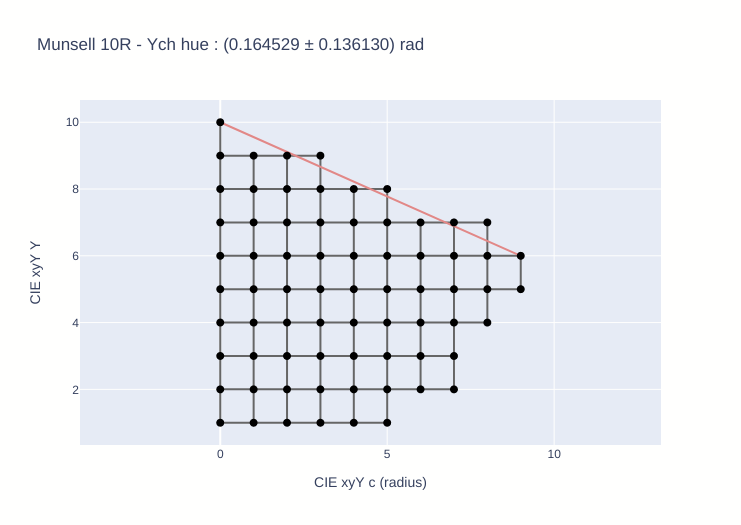
Our goal will be to warp the chromaticity plane to get the test data spaced like our objective, using only invertible transforms. The Munsell colors are given virtual coordinates in our virtual target space, as Yuv components.
#Chromaticity model
We will re-use the formalism of MacAdam moments17 as extended by Pridmore18 for saturation and brightness. These very little-known papers (66 and 16 citations respectively in Google Scholar as of early 2022) start with a quite elegant way to predict the luminance gain necessary to obtain an achromatic colour when mixing two complementary chromaticities, and more generally predicting the result of mixing any number of chromaticities in an additive setup.
The moment of a boundary chromaticity $\lambda$ (belonging to the visible locus boundary) of cordinates $(x, y)$, relative to the achromatic locus (white reference) $(x_n, y_n)$, in CIE xyY 1931 space can be defined as:
$$m_\lambda = \frac{\sqrt{(x - x_n)^2 + (y - y_n)^2}}{y}$$
Similarly, for the complementary boundary chromaticity $\lambda_c$ of coordinates $(x_c, y_c)$ (complementary in the sense that $(x, y)$ and $(x_c, y_c)$ are colinear with the neutral achromatic locus):
$$m_{\lambda c} = \frac{\sqrt{(x_c - x_n)^2 + (y_c - y_n)^2}}{y_c}$$
Then, MacAdam predicts that the ratio between the luminances $L$ and $L_c$ necessary for $\lambda$ and $\lambda_c$ to mix into an achromatic color is :
$$b = \frac{L_c}{L} = \frac{m_\lambda}{m_{\lambda c}}$$
That is to say that the complementary chromaticity $\lambda_c$ has to be gained at a luminance of $b\cdot L$ for the color mix to yield:
$$ \begin{bmatrix} L \\ x \\ y \end{bmatrix} + \begin{bmatrix} bL \\ x_c \\ y_c \end{bmatrix} = \begin{bmatrix} L + bL \\ x_n \\ y_n \end{bmatrix} $$
Pridmore18 refines this one step further by identifying that the relative saturation is the reciprocal of the relative lightness between two complementary boundary colors :
$$b = \dfrac{m_\lambda}{m_{\lambda c}} = \dfrac{L_c}{L} = \dfrac{S}{S_c}$$
From which he derivates the colour attributes brightness and saturation for boundary colours:
$$ \begin{align} B &= L × b \\ S_{B, CIE} &= m × b^2 \end{align} $$
So I will create an ($u, v$) space where the distance to achromatic is equal to the moment $m = \frac{\sqrt{(x - x_n)^2 + (y - y_n)^2}}{y}$ and then linearly map it in 2D in order to better fit Munsell hues and chromas. Notice that the moments method works the same in any CIE radiometric space, and that any linear map preserves the euclidean distance unchanged, which is ground to improve the Munsell fitting some more, in moments space.
#Metrics
Since our ultimate goal is to manipulate saturation and because we don’t want to map the lightness axis, we will be fitting the saturation correlate $\frac{C}{L}$ against the Munsell saturation $\frac{C / 20}{V / 10}$. The Munsell values and chroma normalization factors are meant to ensure C and V are normalized between $[0;1]$. We will minimize the quadratic error over the relative chromaticities $\frac{u}{L}$ and $\frac{v}{L}$ to account for the 3rd orthogonal dimension in the 2D mapping problem and to make a 1D correlation appear between Munsell saturation and our model’s ratios of $\frac{c}{L}$.
#Optimization
The first stage is a global optimization for chromaticity coordinates $(u, v)$. We interleave linear 2D matrix products and the non-linear moment normalization, using a non-linear least-squares solver with a cost function $z = \sqrt{(u_{model} - u_{Munsell})^2 + (v_{model} - v_{Munsell})^2} / L$. The method used is the Trust Region Reflective19 as implemented in the Python numerical library Scipy .
We first convert from CIE XYZ 1931 2° adapted for illuminant CIE D65, then to xyY. The mapping from $Y$ to $L$ is done using the equation $\ref{L-eqn}$. Then, the mapping from xy to uv chromaticities is done using :
$$ \begin{bmatrix} u \\ v \end{bmatrix} = M_1 \cdot \begin{bmatrix} x - x_{D65} \\ y - y_{D65} \end{bmatrix} \\ $$
$$ M_1 = \begin{bmatrix} 2.0265488 & -1.23424972 \\ 0.51328342 & 1.36974324 \end{bmatrix} $$
Following this, we can rewrite the radial distance to achromatic as the moment. Unfortunately, using the MacAdam moment (relative to the $x$ axis), that is dividing the radial distance to achromatic by the $y$ coordinate, distorts the chromaticity in a way that cannot be perceptually fitted for uniform delta E, sending the blue region far away from the rest of similar chromas.
So we compute the moment compared to the $u$ axis, that is using the $v$ coordinate as a divider. But since the $v$ coordinates are remaped in $[-0.5, 0.52]$, we need to find an offset of $v$ against which evaluating the moments to reduce the delta E error. The best fit is found for $v = -0.85937617$ :
$$ \begin{align} \theta &= \arctan\left(\frac{v}{u}\right)\\ u’ &= \frac{\sqrt{u^2 + v^2}}{v + 0.85937617} \cos(\theta)\\ v’ &= \frac{\sqrt{u^2 + v^2}}{v + 0.85937617} \sin(\theta) \end{align} $$
This is shown only for completeness, but since $\cos(\theta) = \frac{u}{\sqrt{u^2 + v^2}}$, we can spare 3 evaluations of transcendent functions and simplify:
$$ \begin{align} u’ &= \frac{u}{v + 0.85937617}\\ v’ &= \frac{v}{v + 0.85937617} \end{align} $$
We then apply a second matrix product to go to UV space :
$$ \begin{bmatrix} U \\ V \end{bmatrix} = M_2 \cdot \begin{bmatrix} u’ \\ v’\end{bmatrix} $$
$$ M_2= \begin{bmatrix} 0.95322837 & -0.15730312 \\ 0.05496097 & 1.04744158 \end{bmatrix} $$
The correlates look good enough:
[gallery columns=“1” link=“file” size=“full” ids=“1417,1418,1420,1419,1421”]
Since we only do 2D vector algebra, the 3 steps above can be simplified into a single rational function that will evaluate faster. The following result is for CIE D65 only (as is the UCS space) :
$$ \begin{align} D &= 0.51328342 \cdot x + 1.36974324 \cdot y + 0.248226918606 \\ U &= \dfrac{1.85102272593919 \cdot x - 1.39198673401947 \cdot y - 0.120851170908779}{D} \\ V &= \dfrac{0.64901548423294 \cdot x + 1.36689046166649 \cdot y - 0.652654103807916}{D} \end{align} $$
The reverse model will be less nice. The first option is to simply use invert the precedent equations :
$$ \begin{align} D &= 0.0545736844628483 \cdot U - 0.946511393183473 \cdot V + 1.0 \\ x &= \frac{0.359179775014519 \cdot U + 0.0524217359106796 \cdot V + 0.3127}{D} \\ y &= \frac{-0.144485240055261 \cdot U + 0.15188423099269 \cdot V + 0.329}{D} \end{align} $$
The second option is to undo the slow track step by step. The first step is to multiply $[U, V]$ by $M_2^{-1}$ :
$$ \begin{bmatrix} u’ \\ v’ \end{bmatrix} = M_2^{-1} \cdot \begin{bmatrix} U \\ V \end{bmatrix} $$ $$ M_2^{-1} = \begin{bmatrix} 1.04006072 & 0.15619467 \\ -0.05457368 & 0.94651139 \end{bmatrix} $$
Then, the reverse moment has 2 solutions because we have to solve a rational polynomial of the second order, which means we have 2 roots and we need to choose the one in the proper quadrant. A key property to solve the reverse model is the fact that moments preserve the angle around achromatic, such that $\arctan2(v, u) = \arctan2(v’, u’)$ therefore $\frac{v}{u} = \frac{v’}{u’}$. Unfortunately, $\frac{v’}{u’} = \frac{-v’}{-u’}$ so we have to check $S_1$ and $S_2$ and choose the one that has the same sign as the non-zero coordinate of the input $(u’, v’)$ :
$$ \begin{cases} S_1 &= \begin{bmatrix} u_1 \\ v_1 \end{bmatrix} = -0.85937617 \cdot \begin{bmatrix} u’ / (v’ - 1) \\ v’ / (v’ - 1) \end{bmatrix} \\ S_2 &= \begin{bmatrix} u_2 \\ v_2 \end{bmatrix} = -0.85937617 \cdot \begin{bmatrix} u’ / (v’ + 1) \\ v’ / (v’ + 1) \end{bmatrix} \end{cases} $$
Finally, multiply by the inverse matrix $M_1^{-1}$ :
$$ \begin{bmatrix} x - x_{D65} \\ y - y_{D65} \end{bmatrix} = M_1^{-1} \cdot \begin{bmatrix} u \\ v \end{bmatrix} $$ $$ M_1^{-1} = \begin{bmatrix} 0.40175829 & 0.36201679 \\ -0.15055075 & 0.5944054 \end{bmatrix} $$
#HDR support
To understand how HDR may affect our model, we need to review the current imaging pipeline design and perform a thought experiment.
In the scene-referred workflow that arose from the needs of alpha compositing (occlusion modelling) and dynamic-range-agnostic workflow, the general goal is to process the radiometrically-scaled image (scene-linear). Indeed, applying image transforms that break the radiometric relation also introduce artifacts in later convolutional filters (blurs) and alpha compositing (opacity/transparency of stacked layers). Therefore, it is desirable to keep the image data radiometrically-scaled for as long as possible along the editing pipeline.
However, as of 2022, most “graphical art” editing displays are still SDR, with a contrast ratio of maximum 1000:1 and a white intensity of maximum 350 Cd/m². Also, photography is still very much grounded in the paper world, where contrast ratios are much lower. So, there is a need for a non-linear view transform that maps possibly HDR imaging pipelines to SDR display. A such transform has been detailed in the 2018 article Filmic, darktable and the quest of the HDR tonemapping. This view transform is to be applied as late as possible in the pipeline.
But this means that the data been manipulated in the image processing pipeline are not directly the data being rendered on the screen. So we need operators affecting pipeline colours in a way that is predictable in terms of results as seen on the screen. Namely, the pipeline white luminance may be 2 to 4 times higher than the display white luminance. This will affect the perceptual attributes of colour, because both lightness and chroma (as per the CIE definition of chroma, which is different from the Munsell chroma, called colorfulness in the CIE referential). This separation between the HDR model, from the inner pipeline, and the SDR view, from the pipeline output, is still one of the most challenging concepts to grasp for image software developers and users alike.
How does an HDR pipeline relate to Munsell colours upon which we have fitted the darktable UCS 22 ?
We could imagine a first Munsell sweep (like a page of the Munsell book of colours), made of reflective material, lit by some light source. If we had a perfect diffuser attached to the sweep (100 % white), it would have a luminance of 100 Cd/m². The implicit part of the Munsell values is they are all defined by comparison with the value of the pure white. Since this value is normalized to unit, the operation is silent and does not appear.
Now, we put another Munsell sweep in the same visual field, but lit with a light source 4 times as bright as the first one (+2 EV). This will shift the reference of white in our visual field and raise it by 2 EV, so all the colours from the first sweep will be redefined in our perception by comparison with the new white reference. Noticeably, the lightness (Munsell grey patches) scale of the first sweep gets compressed non-linearly, and so do its chroma. In other words, the comparison to pure white is not silently normalized by 1 as far as the first sweep is concerned.
In darktable’s pipeline, we work in a scene-referred workflow where users are expected to normalize linearly the RGB code values such that the reflective middle-grey (20 %) is anchored at 0.20 and the perfect reflective white (100 %) at 1. Values above 1 are the realm of specular highlights, emissive surfaces or reflective elements lit by a secondary light. When the whole image is made of reflective materials lit at different intensities, the diffuse white reference is the one relative to the lighting of the region of interest, which will be the subject of the picture in most cases. For example, for a picture of a subject in a backlit situation, we consider the reflective range $[0;1]$ relatively to the bounce light lighting the side of the subject exposed to the photographer’s lens.
All this means that the perceptual colour attributes will need to be adapted for the scene SDR white. Adaptation involves defining a reference to which adapt the test samples. As the vast majority of screens are still working in SDR and as our UCS is fitted on Munsell reflective colours, we will normalize the colour attributes to the realm of Munsell colours : the reflective range $[0; 1]$ where 1 is assumed to be the relative luminance of the perfect white diffuser.
This means that we will have to backport some of the adapting properties of CIE CAM 16 and translate them.
#Colour attributes
We assume an average viewing background, meaning a 20 % middle grey compared to the perfect diffuser luminance. This will allow us to simplify the CIE CAM 16 colour attributes and is the recommended background in darktable as of v3.0 and above, and also meets the ISO standard for pre-press (REFERENCE).
#Lightness-Chroma model
The lightness-chroma model is the easiest to derivate from Munsell colours. We will introduce the adapting values by analogy with CIE CAM16.
#Lightness
The simplified CIE CAM1615 defines the lightness $J$ as follow:
$$J = \left(\frac{A}{A_{white}}\right)^{cz}$$
where $A$ is the achromatic response, and $cz$ accounts for the Stevens effect. Then, $z = 1 + \sqrt{n}$ and $c = 0.69$ for an average viewing surround.
$n$ is defined as the ratio of luminances between the background and the accepted white in the conditions of viewing, such that $n = \frac{L_{background}}{L_{white}}$. For normal conditions, $L_{background} = 0.2$ (middle-grey referred to diffuse white) and $L_{white} = 1$ (diffuse white), which yields $n = 0.2$, $z = 1.4472$, and finally $cz \approx 1$. So it appears that $c$ is adjusted for $cz$ to be a no-operation in normal conditions.
While the conditions of viewing can be assumed to be average if the image editor follows ISO recommendations for photography and pre-press worflows, the white level is the one from the possibly HDR scene and will need to be accounted for. I have shown that the $L^*$ coordinate of the darktable UCS correlates with CIE CAM16 $A$, so we will backport this formula from CIE CAM16:
The lightness $J$ in darktable UCS will be defined as follow :
$$J = \left(\frac{L^*}{L^*_{white}}\right)^{cz}$$
where $c$ and $z$ have the same meaning as in CIE CAM16. $L_{background}$ can be assumed to be 20 % all the time, since even HDR images tend to have an average luminance close to middle-grey. $L_{white}$ needs to be radiometric luminance of the scene-referred white of the picture. $L^*_{white}$ is the non-linearily adapted correlate of Munsell value corresponding to the white point of the picture, and $L^*$ is the pixel-wise correlate of Munsell value. Recall that $L^*$ metrics correlated to Munsell value are adjusted such that diffuse white (usually anchored between 80 and 120 Cd/m²) is normalized to 1, so for a purely reflective scene lit evenly, $J = L^*$ directly.
#Colorfulness
The colorfulness as defined by the CIE is an absolute metric, which corresponds to the radial distance to achromatic. We can compute it directly :
$$ M = \sqrt{U^2 + V^2}\label{eqn-colorfulness}$$
#Chroma
The chroma has been largely misunderstood among programmers as the same thing as colorfulness, but the CIE defines it as relative to white. Many models like CIE Lab or CIE Luv and so on are bounded by diffuse white and since diffuse white is normalized to 1 or 100 %, chroma becomes to all intents and purposes colorfulness. But the concept remains : chroma is colorfulness divided by the achromatic response of white, and the fact that this response being normalized to 1 makes the division pointless doesn’t change it.
In darktable UCS, the Munsell chroma is only weakly correlated to colorfulness ($R^2 = 0.73$). Before carrying on, I propose to improve the 1D correlate by fitting $C = f(M, L)$. The proprosed chroma correlate is :
$$ \begin{cases} C &= 0 &\text{ if } L = 0 \\ C &= \frac{2.78288575869163}{L^*_{white}} \cdot \left(L^* \left(\dfrac{M}{L^*}\right)^{0.648780286421352}\right)^{1.73754096076991} &\text{else} \end{cases}\label{eqn-chroma} $$
#Objective evaluation
#Plots
I plot below the Munsell colours into darktable UCS $(L^*, C)$ planes of constant hue :
This shows some interesting properties of the colour space :
| Munsell hue | Oklab hue deviation | dt UCS hue deviation | Oklab saturation deviation | dt UCS saturation deviation |
|---|---|---|---|---|
| 10 RP | 0.116 | 0.128 | 0.179 | 0.029 |
| 2.5 R | 0.109 | 0.115 | 0.162 | 0.025 |
| 5 R | 0.109 | 0.115 | 0.164 | 0.030 |
| 7.5 R | 0.113 | 0.122 | 0.163 | 0.031 |
| 10 R | 0.128 | 0.135 | 0.163 | 0.030 |
| 2.5 YR | 0.111 | 0.115 | 0.130 | 0.021 |
| 5 YR | 0.081 | 0.090 | 0.100 | 0.019 |
| 7.5 YR | 0.074 | 0.074 | 0.091 | 0.017 |
| 10 YR | 0.062 | 0.071 | 0.087 | 0.019 |
| 2.5 Y | 0.045 | 0.060 | 0.082 | 0.018 |
| 5 Y | 0.044 | 0.050 | 0.078 | 0.018 |
| 7.5 Y | 0.029 | 0.027 | 0.077 | 0.017 |
| 10 Y | 0.020 | 0.013 | 0.076 | 0.016 |
| 2.5 GY | 0.026 | 0.024 | 0.075 | 0.014 |
| 5 GY | 0.047 | 0.057 | 0.084 | 0.013 |
| 7.5 GY | 0.047 | 0.063 | 0.089 | 0.015 |
| 10 GY | 0.051 | 0.071 | 0.107 | 0.024 |
| 2.5 G | 0.063 | 0.068 | 0.136 | 0.029 |
| 5 G | 0.054 | 0.057 | 0.140 | 0.020 |
| 7.5 G | 0.048 | 0.051 | 0.141 | 0.015 |
| 10 G | 0.043 | 0.054 | 0.141 | 0.011 |
| 2.5 BG | 0.050 | 0.076 | 0.136 | 0.011 |
| 5 BG | 0.058 | 0.104 | 0.121 | 0.010 |
| 7.5 BG | 0.054 | 0.110 | 0.116 | 0.017 |
| 10 BG | 0.060 | 0.126 | 0.112 | 0.030 |
| 2.5 B | 0.058 | 0.126 | 0.113 | 0.043 |
| 5 B | 0.055 | 0.125 | 0.118 | 0.057 |
| 7.5 B | 0.072 | 0.120 | 0.135 | 0.067 |
| 10 B | 0.101 | 0.097 | 0.138 | 0.071 |
| 2.5 PB | 0.118 | 0.070 | 0.158 | 0.076 |
| 5 PB | 0.148 | 0.052 | 0.186 | 0.082 |
| 7.5 PB | 0.107 | 0.096 | 0.564 | 0.197 |
| 10 PB | 0.089 | 0.063 | 0.422 | 0.120 |
| 2.5 P | 0.077 | 0.045 | 0.356 | 0.100 |
| 5 P | 0.060 | 0.033 | 0.300 | 0.080 |
| 7.5 P | 0.020 | 0.040 | 0.256 | 0.070 |
| 10 P | 0.045 | 0.073 | 0.226 | 0.060 |
| 2.5 RP | 0.069 | 0.099 | 0.210 | 0.052 |
| 5 RP | 0.097 | 0.124 | 0.196 | 0.040 |
| 7.5 RP | 0.105 | 0.124 | 0.179 | 0.029 |
| TOTAL | 0.4948 | 0.5590 | 1.20 | 0.35 |
Lower errors diverging by more than 5% of relative magnitude are emphasized.
The darktable UCS space shows a globally superior hue-linearity error, except in the purple-blue region. It is still very close (within ±5%) from Oklab in the red, yellow and green region. I didn’t try hard to fit for hue-lineary and Abney effect since no dataset of constant hue loci seems to agree with the others, except on the fact that yellow (570 nm, roughly Munsell 10 Y) is a straight line in CIE xyY :

As it turns out, the Munsell 10Y is also the minimum of hue average deviation for both models.
Where the darktable UCS actually shines is in its correlation to Munsell saturation, taken as the RMSE between $\frac{\text{Munsell chroma} / 20}{\text{Munsell value} / 10}$ and $\frac{\text{model chroma}}{\text{model lightness}}$. This models the scaling of the chroma axis relatively to the lightness axis, and therefore the 2D uniformity of the delta E. It is of critical importance since we are planning to travel $(L, c)$ plane in diagonal directions. The darktable UCS not only has a lower saturation error, but it is more evenly distributed along the visible locus. This can also be observed from the graphs of constant hue, where the mesh formed by lines of equal lightness and equal chroma appears more square in darktable UCS than in Oklab.
The overall better behavious (hue linearity and saturation error) of darktable UCS is notable in the blue-purple region, which is the typically pathological point of all perceptual colour spaces and the region where the worst out-of-gamut colours appear in display RGB. This makes it much more stable for future gamut-compression tasks.
#Predictions
The next thing to assess is how opponent additive colours are recorded in terms of hue. I have already shown in the sRGB book of colour that, in JzAzBz, the cyan complementary of sRGB/Rec709 red is not over a -180° hue angle fom the sRGB red. The property of opponent colours to produce achromatic light makes for a much more robust definition of colour opponency.
| Colour | sRGB coordinates | Luminance Y | Oklab hue | darktable UCS hue | darktable UCS colorfulness |
|---|---|---|---|---|---|
| Red | $(1, 0, 0)$ | 0.214 | 29° | 19° | 0.7659 |
| Yellow | $(1, 1, 0)$ | 0.927 | 110° | 101° | 0.3640 |
| Green | $(0, 1, 0)$ | 0.713 | 142° | 137° | 0.5977 |
| Cyan | $(0, 1, 1)$ | 0.786 | -165° | -160° | 0.2504 |
| Blue | $(0, 0, 1)$ | 0.073 | -95° | -79° | 1.2673 |
| Magenta | $(1, 0, 1)$ | 0.287 | -32° | -42° | 0.6752 |
So we can verify the hue angle of opponent colours :
| Mix | Oklab | darktable UCS | $Y_1 / Y_2$ | $M_2 / M_1$ |
|---|---|---|---|---|
| Red → Cyan | 29° - (-165°) = 194° | 19° - (-160°) = 179° | 0.272 | 0.327 |
| Yellow → Blue | 110° - (-95°) = 205° | 101° - (-79°) = 180° | 12.70 | 3.482 |
| Green → Magenta | 142° - (-32°) = 174° | 137° - (-42°) = 179° | 2.484 | 1.130 |
#Synthetic sweeps
Here are hue stripes produced at constant chroma and lighntess. Stripes are distributed at uniform lightness steps. The chroma is adjusted on each stripe to be as high as possible while remaining inside sRGB space.








The next gradients are hue × lightness at constant chroma. The colours that did not fit within sRGB gamut have been replaced by white.
Finally, the sRGB gamut slices at constant hue containing the primary Red/Cyan, Green/Magenta and Blue/Yellow


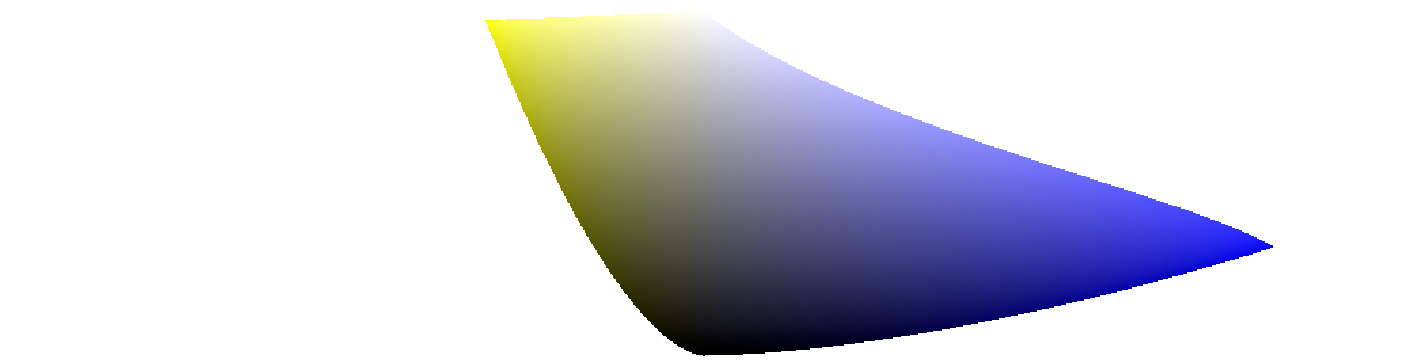
The last one, blue-yellow, clearly shows the Abney effect : from pure blue, the gradient takes a leap toward purple. This means that I will have to adjust hues some more after all.
#Hue
#Fitting hue
So far, we have considered the angle on the chromaticity plane $(U, V)$ to be the correlate of hue. We know that it is not completely perceptually accurate, but has the desirable property of keeping opponent colors set aside at 180°, which will be of use for the Brightness-Saturation model. Unfortunately, the sRGB blue gamut slice shows that this is not good enough to manipulate colors at constant hue.
All colour adaptation models deal with hue-linearity by tuning the LMS cone response. That is, each cone response is modeled in a 3D space from the radiometric emission (usually, going through CIE XYZ 1931), and then adapted through a non-linear transform. The product of this, as I showed above, has 2 properties :
- LMS cone space can and will output negative values for positive stimuli,
- complementary colours don’t have an angle of 180° anymore,
- the equi-lightness plane gets slanted.
However, linearizing hue perceptually will be where we pay the price of the previous choices : it will be heavily non-linear, and there is only so much we can do if we choose to ignore the retina’s physiology to work at constant lightness. Finally, the constraint of invertibility prevents us from using excentricity functions of hue like $e(h_{UCS}) = K \cdot \sum_{i=1}^{n} a_i \cos(i\cdot h_{UCS}) + b_i \sin(i \cdot h_{UCS})$, which is typically used to correct colorfulness or chroma by Hunt’s, CIE CAM16 and Nayatani’s models. Correcting hue as a function of itself would be the easiest way, but it is not a bijection and cannot be inverted.
First, we will need to remap the UCS with regard to chroma. Recall that the colorfulness $M$ is the “naive” radial distance to achromatic (equation $\eqref{eqn-colorfulness}$) in $L^*UV$ space. The chroma correlate $C$ is expressed by the equation $\eqref{eqn-chroma}$ as a function of $M$ and $L$. Then:
$$ \begin{align} \theta &= \arctan2(V, U)\\ \begin{bmatrix} U’ \\ V’ \end{bmatrix} &= \begin{bmatrix} C \cos(\theta) \ C \sin(\theta) \end{bmatrix} \end{align} $$
Then, we warp the $(U’, V’)$ space to center it on what appears to be the perceptual center of hues:
$$ \begin{bmatrix}U’’ \\ V’’\end{bmatrix} = M_3 \cdot \begin{bmatrix} U’ \\ V’ \end{bmatrix}\\ $$ $$ M_3 = \begin{bmatrix} 0.76426712090492599 & 0.20054726807320489 \\ -0.16136815864400481 & 0.55140064490679086 \end{bmatrix} \cdot $$
Then, we adapt non-linearily the $(U’’, V’’)$ space using independent Michaelis-Menten equation :
$$\begin{align} \alpha &= sign(U’’) \frac{0.74620661742486705 \cdot |U’’|^{1.1091628757564669}}{|U’’|^{1.1091628757564669} + 1.2697466043995993} \\ \beta &= sign(V’’) \frac{1.2008251904267178 \cdot |V’’|^{1.0640450648317035}}{|V’’|^{1.0640450648317035} + 1.429978004863145} \end{align}$$
Finally, we express the hue angle and its distance to the center of the space, which is not achromatic anymore, because of the $O$ offset:
$$ \begin{align} r &= \sqrt{\alpha^2 + \beta^2} \\ \gamma &= \arctan2(\beta, \alpha) \\ H &= 1.0373679054932574 \cdot \gamma + 0.32440889433879067 \end{align} $$
Notice that the radius $r$ is not a direct correlate of chroma anymore, because our space warping has essentially made Munsell chroma circles elliptic again, for the sake of hue-linearity. So $r$ is to be considered as an intermediate variable stored only to make the refined hue correlate invertible to original chroma and angle.
This radius $r$ can be easily fitted once again against Munsell chroma, with the following model:
$$ \begin{align} E(H) =& i + a \cos(H) + b \sin(H) + c\cos(2H) + d \sin(2H) \\ &+ e \cos(3H) + f \sin(3H) + g\cos(4H) + h \sin(4H) \nonumber\\ C’ =& 2.6966804 \cdot (E(H) \cdot r)^{1.26617339} \label{eqn-chroma-r} \end{align} $$
with:
- $a = 0.1168930$
- $b = 0.08057494$
- $c = 0.06451043$
- $d = 0.00929771$
- $e = -0.11172693$
- $f = -0.11981897$
- $g = 0.03453699$
- $h = 0.08214589$
- $i = 1.44146029$
The correlation is very good, with $R^2 = 0.97$ :
The improved accuracy is mostly due to the excentricity factor $e(H)$, because setting $e(H) = 1$ and fitting for the two remaining parameters yields an $R² = 0.929$, which is worse than $C$ at the previous step. This is actually consistent with the fact that Munsell chroma circles have been made elliptic in this hue-linear space
Going to the refined chroma estimate $C’$ to the radius $r$ is done with the following equation:
$$r = \left(\dfrac{C}{2.6966804}\right)^{1 / 1.26617339} \cdot \dfrac{1}{E(H)}$$
where $E(H)$ is the excentricity gain as defined above.
The reverse transform yields:
$$ \begin{align} \gamma &= \frac{H - 0.32440889433879067}{1.0373679054932574} \\ \alpha &= r \cos(\gamma)\\ \beta &= r \sin(\gamma)\\ U’’ &= sign(\alpha) \left(\frac{-1.2697466043995993 * |\alpha|}{|\alpha| - 0.74620661742486705}\right)^\frac{1}{1.1091628757564669} \\ V’’ &= sign(\beta) \left(\frac{-1.429978004863145 * |\beta|}{|\beta| - 1.2398430649704526}\right)^\frac{1}{1.0640450648317035} \\ \begin{bmatrix}U’ \\ V’\end{bmatrix} &= \begin{bmatrix} 1.2151295 & - 0.44194889 \\ 0.35560932 & 1.6842264 \end{bmatrix} \begin{bmatrix}U’’ \\ V’’\end{bmatrix} \\ \theta &= \arctan2(V’, U’) \\ C &= \sqrt{U’^2 + V’^2} \end{align} $$
It is worth noting that we now have a $(\theta, C)$ space of even chroma (circular Munsell chroma rings), defined at the previous step, where $\theta$ is an inaccurate correlate of hue, and a $(H, r)$ space of even hue (linear Munsell hue lines) where $r$ is an inaccurate correlate of chroma. Both spaces are half-specified in terms of perceptual correlates. Additionnaly, complementary colours are not set apart by an angle of 180° in this space, so it looses any additivity property for complementary colours. However, it gets much better perceptual evenness.
#Manipulating real colours at constant hue and chroma
If we are to manipulate both chroma at constant hue and hue at constant chroma from an original known colour, we need to interleave both models:
On the above principle schematic, the black coordinates refer to the $(\theta, C)$ space and the grey coordinates refer to the $(H, r)$ space. $W_C$ is the origin of the $(\theta, C)$ space, which is D65 illuminant by design, and $W_H$ is the origin of the $(H, r)$ space, moved from D65 at constant lightness by an offset defined in the vector $O$ above. The blue dotted curves represent the loci of constant hues in $(\theta, C)$ space, which the $(H, r)$ aims at making straight for better handling.
Suppose we start at a point of coordinates $(C_1, H_2)$ and we want to map this point for artistic purposes to a new colour of coordinates $(C_2, H_3)$. The point $(C_1, H_2)$ is first expressed in $(\theta, C)$ space by the coordinates $(\theta_1, C_1)$. Since $\theta_1$ cannot be trusted as a correlate of hue, we have to project it to $(H, r)$ space and record its hue $H_2$.
We move to $C_2$ following the radial direction $\theta_1$ in $(\theta, C)$ space. The new coordinate is $(\theta_1, C_2)$ but it has a wrong hue $H_1$ because the $(\theta, C)$ space is not hue-linear. So we need to project $(\theta_1, C_2)$ to the $(H, r)$ space and record its coordinate $(H_1, C_2)$. In there, we substitute the wrong hue $H_1$ with the original hue $H_2$ to get the point $(H_2, C_2)$, which has the new expected chroma at the same hue as the original.
Now comes the hue mapping. From the point $(C_2, H_2)$ expressed in $(H, r)$ space as the coordinates $(H_2, r_2)$, we need to rotate around $W_H$ by an angle $H_3 - H_2$ following along the radius $r_2$. The radius $r_2$ is by no mean a metric of chroma, so the resulting color will have the proper destination hue $H_3$ but a wrong chroma. We could just project the point $(H_3, r_2)$ to the $(\theta, C)$ space and substitute the wrong chroma with $C_2$, but that would be inaccurate because the chroma change would make the colour travel toward $W_C$, meaning the final hue would not be $H_3$. This may be accurate enough in most cases though. To get a proper chroma mapping at constant hue, we would need to solve the equation $C_2 = r_3$ for $r_3$, and then substitute $r_2$ for $r_3$ in $(H, r)$ space.
Alternatively, the correlate of chroma $C’$ can be directly derivated from $r$ using equation $\eqref{eqn-chroma-r}$ and its inverse, then everything can be manipulated from $C’$ and $H$, then converted to $(H, r)$, then to $(\theta, C)$, then finally to Yuv through the reverse chroma → colorfulness.
Fortunately, there are few use cases in actual image processing that require to rotate hues, and most of them are currently done in HSL or Yuv spaces with no complains from users, so the inaccurate way is more likely enough.
#Expressing synthetic colours from perceptual hue and chroma
To create uniform GUI gradients, colour charts and sweeps, we create synthetic colour in perceptual spaces from scratch and project them to display RGB. If we want to define a colour by specifying both its hue and chroma perceptual correlates, we need to use both $(\theta, C)$ and $(H, r)$ spaces, but that will leave us with $r$ and $\theta$ unspecified. To project this colour back to a display space, we need to fill at least a third component such that we have at least one complete set of coordinates in one space. From there, the transforms between spaces are fully defined and revertible.
A synthetic colour of perceptual attributes $(H_s, C_s)$ would have, in each space, the following coordinates:
$$ \begin{bmatrix} H_s \\ C_s \end{bmatrix} \equiv \begin{bmatrix} H_s \\ r_s \end{bmatrix}_{H, r} \equiv \begin{bmatrix} \theta_s \\ C_s \end{bmatrix}_{\theta, C} $$
in which $H_s$ and $r_s$ and both dependent variables from $\theta_s$ and $C_s$. Because of the non-linear transforms containing sign and absolute value heuristics, we cannot express directly nor simply $r_s$ from $C_s$ and $\theta_s$. However, we have expressed above in $\eqref{eqn-chroma-r}$ $C$ as a function of $r$ with a good fitting, and its inverse. Using this method to generate synthetic hue charts yields a more uniform chroma, noticeably more colorful blues compared to other hues (examples below at chroma = 25%):


#Synthetic sweeps at improved hue constancy
Hue sweeps at increments of $L^* = 10$. Chroma has been adjusted to the maximum value that fit in sRGB gamut. Compared to the previous stage ($C$ non adjusted for hue with the excentricity equation), the chroma had to be divided by a factor of roughly 1.6 to fit within sRGB gamut, because the blue region fell outside.









Next, we review the sRGB gamut at constant hue. The first approach is to sweep over radius $r$ and lightness, in $(H, r)$ space:



The gamut is compressed over the chroma axis, which is the trade-off we made for improved hue linearity. This works, as it shows on the blue-yellow, since the gradient from achromatic to sRGB primary blue does not take a leap toward purple anymore. As stated above, the radius $r$ is no longer a direct correlate of chroma, and this can be an issue. We can resolve that with a second approach, by sweeping over chroma as defined as $C’$ and hue as $H$, then using equation $\eqref{eqn-chroma-r}$ to go to $H, r$ space from which we convert to $\theta, C$ space, then back to colourfulness $M$ and YUV. This is shown in the next sweeps, where sRGB colours are displayed in real colours, and colours within the visible locus but outside of sRGB are represented in grey. The scale of both axes is normalized to unit, so the delta E is theoritically circular :
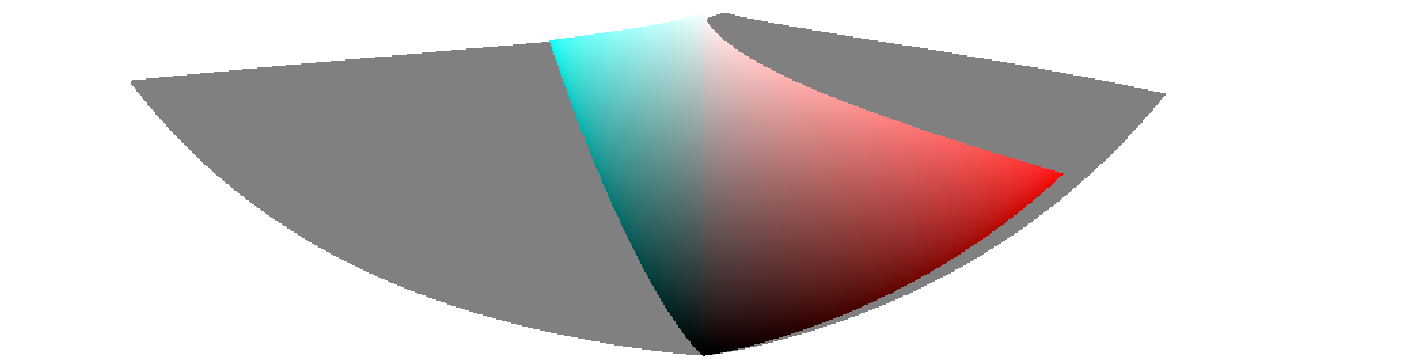


The conclusion from these results is that the $(H, r)$ space is worthless on its own and has merits only as a connection space to the $(H, C’)$ space. This last space has a chroma cusp at the achromatic locus which may be challenging and ill-suited for synthetic gradients that go through achromatic, in which case the chroma correlate $C$ will need to be substituted from the $(\theta, C)$ space, giving a less accurate correlation but smoother.
Though none of the $(H,r)$ and $(H, C’)$ spaces have complementary colours at opposite hue angles (set apart by 180°), the absolute deviation for sRGB primaries is only between 6° and 8° of angle.
#Brightness-Saturation model
The lightness-chroma we have built so far shows good color uniformity, that is a fairly even delta E (colour difference) as well as a good relative scaling between chroma and lightness. We could then quickly express saturation as colourfulness / brightness, but then, how to express brightness ?
To understand the problem we are facing, let us review hue patches against a background having the same lightness (you are advised to open each image in a new tab and look at it full-screen). In each of the following sweeps, all colours in a row have the same chroma (as predicted by the darktable UCS) and the same lightness, which is also the lightness of the neutral background :




Even though the lightnesses are all the same on the same row, they don’t feel the same : orange, purple-red and turquoise feel more luminous than the others and than the background. So, at constant chroma and lightness, their brightness is different. This is the Helmholtz-Kohlrausch effect. The main reason is chroma and lightness are evaluated against white (which actually shows in the equations) while brightness is evaluated against a grey of the same lightness. But it does not stop there :







Above, we make chroma vary between 10% and 90% at $L^* = 50%$ against a background at $L^* = 50%$. The colours that could not be represented in sRGB gamut have been removed. Here, we see that colours start feeling fluorescent above a certain chroma threshold. This effect is called “fluorence” by Evans & Swenholt11, and the threshold at which it appears is the greyness boundary. In other words, past the greyness boundary, colorful objects appear fluorescent against a background having the same lightness.
From this, we understand several things:
- chroma or colorfulness participates in brightness too, along with lightness,
- the weight of the contribution of colorfulness in brightness depends on hue,
- manipulating chromas for artistic purposes may not have the desired effect on saturation, e.g. it may make some hues cross the greyness boundary quicker than others even in a perceptually-uniform space.
So the purpose of the brightness-saturation model is to take these effects into account.
#Fitting brightness
The Pridmore17 model was first attempted because of its intrinsic elegance, its dependency on first principles and its serious advantage regarding the prediction of complementary colours under the assumption that a mixture of complementary lights at correct luminance (adjusted with MacAdams method13) yields achromatic light. The complete model used was:
$$ \begin{align} Moment(x, y) &= \dfrac{\sqrt{(x - x_n)^2 + (y - y_n)^2}}{y}\\ S_\lambda &= \sqrt{\dfrac{Moment(x_\lambda, y_\lambda)}{Moment(x_{\lambda,c}, y_{\lambda, c})}}\\ b_\lambda &= 1.5 \times S_\lambda^{0.25} \\ p_{ct} &= \left(\dfrac{0.054}{b_{max} \times S_\lambda}\right)^{0.79} \\ f &= \dfrac{0.027}{p_{ct}} \\ p &= \dfrac{C}{C_\lambda} \\ F &= \sqrt{\dfrac{p - p_{ct}}{1 - p_{ct}}} \times (1 - f) + f \\ g &= \sqrt{\dfrac{\max(S_\lambda)}{S_\lambda}} \\ F_g &= \dfrac{F + g - 1}{g} \\ b &= 1.5 \times S_\lambda^{0.27} \times p \times F_g + (1 - p) \\ B &= b \times L \\ S &= b^2 \times Moment(x,y) \end{align} $$
where:
- $B$ is the brightness,
- $S$ is the saturation,
- $(x, y)$ are the CIE 1931 xyY chromaticity coordinates of the current colour being evaluated,
- $(x_n, y_n)$ are the CIE 1931 xyY chromaticity coordinates of the achromatic reference (illuminant),
- $(x_\lambda, y_\lambda)$ are the CIE 1931 xyY chromaticity coordinates of the monochromatic wavelength associated with the current chromaticity (boundary colour of the visible locus colinear with $(x_n, y_n)$ and $(x, y)$),
- $(x_{\lambda,c}, y_{\lambda, c})$ are the CIE 1931 xyY chromaticity coordinates of the complementary colour of $(x_\lambda, y_\lambda)$ (boundary colour of the visible locus colinear with $(x_\lambda, y_\lambda)$ and $(x_n, y_n)$),
- $p$ is the purity associated with $(x, y)$ such that $p(x_n, y_n) = 0$ and $p(x_\lambda, y_\lambda) = 1$, and $p$ is perceptually scaled between the achromatic and boundary colours. Therefore, we use the chroma $C$ from the darktable UCS and normalize it by $C_\lambda$, the chroma of the associated boundary colour,
- $p_{ct}$ is the purity threshold corresponding to a Just Noticeable Difference between achromatic light and chromatic light for the current hue.
The numerical constants can be tuned to better match experimental datasets. However, this model suffers from an important limitation : it cannot be inverted. Indeed, it has a double and non-linear dependency to the distance to achromatic, through the purity $p$ (derivated from $C$) and the MacAdams moment. More importantly, this distance is expressed in different spaces, so there is no closed-form expression that could allow to manipulate the colour saturation and brightness, then bring it back to XYZ.
So I need to find something else.
It is useful to note that the Hunt model, inherited by CIE CAM97 and finally by the Hellwig-Fairchild-Stolitzka20 modification to CIE CAM16 correct the non-linear lightness of the achromatic signal $J_A$ for Helmholtz-Kohlrausch effect as follow:
$$J_{HK} = J_A + \alpha C^\beta$$.
That is, a linear combination of chroma and achromatic lightness, with an optional non-linear compression applied on chroma depending on models. The Pridmore model applies a gain over the linear (non adapted) achromatic lightness. If we accept that the non-linear cone adaptation based on Naka-Rushton/Michaelis-Menten resembles in principle a logarithm, then:
$$ \begin{align} B &= b(C) \times L \\ \Rightarrow \log(B) &= \log(b(C)) + \log(L) \\ \equiv J_{HK} &= \alpha C^\beta + J_A \end{align} $$
So the two formulations might well be the same equation seen from a logarithmic or from a linear vantage point. After trial-and-error modelling over the darktable UCS, I propose the following model:
$$B = (1 + 0.10111571 \times C’) \times J$$
where $C’$ is taken from the chroma refinement (equation $\eqref{eqn-chroma-r}$) at constant hue $H$, from the $(H, r)$ space. For neutral colours, $C’ = 0$ which yields $B = J$ as expected.
The fitting was done against 2 datasets:
- Withouck et Al. (2013)21 : 9 observers matching the luminance of the achromatic light in temporal juxtaposition with chromatic light at 51 Cd/m² in dark conditions (unrelated stimuli) – 58 samples
- Sanders & Wyszecki (1963)22: 20 observers matching the luminance of the achromatic light against chromatic lights at 20 Cd/m² in average conditions (related stimuli) – 96 samples.
The validation is done against 2 more datasets:
- Fairchild & Pirotta (1990)23: 11 observers matching reflective paper tiles of Munsell colours matched against neutral tiles at variout lightnesses in average conditions (related stimuli) — 36 samples,
- Wyszecki (1967)24: 76 observers matching ceramic tiles of Munsell colours against neutral tiles at around 30 Cd/m² in average conditions (related stimuli) – 43 samples.
Notes :
- Chromaticity coordinates for Withouck et Al. (2013) and Sanders & Wyszecki (1963) are given for the CIE 1964 10° observer, while the two other studies provide chromaticity coordinates for the CIE 1931 2° observer. An attempt to derivate an approximate matrice transform from synthetic spectra, using color matching functions, to express all data in CIE 1931 2° was made and led to worse fitting than using no correction, so it was abandoned and the datasets are used as-is.
- Studies use various synthetic and natural illuminants resembling CIE C illuminant, but with CCT varying from 6200 to 6900 K. No attempt was made to normalize illuminants to D65 since 3 over 4 studies use a mixture of artificial and natural illuminants.
- While the Withouck et Al. (2013) is the only experiment done in dark surround, adapting to Stevens effect through the CIE CAM16 correction led to worse fitting, so it was abandonned as well.
The graph above shows the fitting of the datasets for the proposed model. It is worth mentionning that the global R² coefficient is 0.77 before any fitting because the different datasets are evenly spread over the luminance axis. The reflective datasets seem irreconciliable with the emissive datasets and any attempted fitting that succeeded on one failed on the other, so the emissive (self-luminous) case was favoured because modern image processing is made on emissive display. The Wyszecki 1967 (reflective) shows a negative R², but looking closer, we see that the cluster of points is indeed aligned with the identity line only with an offset. This may point towards experimental mistakes and will not be investigated further. Finally, the Fairchild & Pirotta datasets shows good correlation only because it is spread over the brightness axis, there is no clear trend shown in the clusters of points.
Withouck et al.21 report that no significant dependency of the Helmholtz-Kohlrausch effect upon hue could be found, while all other models (Hunt, CIE CAM16, Nayatani and Hellwig modified CIE CAM1620) use an excentricity factor to correct chroma for hues. I second this observation but I would like to point that I use an excentricity factor on the chroma correlate $C’$ earlier in the model. This might only indicate that other models have a poor fitting of the chroma correlate in the first place, and the HKE only makes this error more obvious to a point where the correction is non-optional. It might be worth considering a fix earlier on the chroma correlate.
Finally, fitting for brightness against $C$ instead of $C’$ (as defined in the first part of the model, lightness-chroma) yields better correlations with experimental data. Since this estimate of chroma is less accurate and not hue-linear, compared to $C’$, it might average experimental discrepancies better.
#Saturation
As per the CIE definition, saturation derivates from chroma and brightness as follow:
$$S = \dfrac{C’}{B}$$
#Synthetic brightness-saturation sweeps
Below, we make hue vary at constant lightness and chroma, then at constant brightness and saturation:




Compared to the lightness-chroma variant, the brightness-saturation variant shows marginally darker red and blue, but the difference is barely perceptible. Bear in mind, however, that this sweeps are displayed on a white background, which is a lightness setting. The next setting is indeed a brightness setting, with hue patches at constant saturation or chroma against a grey background having the same lightness or brightness (50 %):


(It is better to open each image in full-screen and to display it against a grey background).
Then, we review saturation sweeps at constant brightness :
The sRGB gamut slices at constant hues and varying saturation and brightness, containing the space primaries follow. In grey, I have represented colours lying within the visible locus but outside the sRGB gamut to get a sense of the visible locus shape on a brightness-saturation plane. The scale of both axes is normalized to unit :



These graphs show a problem. Recall that our original goal was an expression of saturation that would smoothly degrade red into white trough all shades of pink, and similarly for all other colours. What we have here is a colorimetric saturation, as per the CIE definition, that is a reweighted chroma for even perceptual brightness, and a brightness that essentially neutralizes the chroma component in the perceived lightness. But moving primary colours toward achromatic still yields grey and that is still not what we are after. We want the painter’s saturation.
However, these graphs show clearly the benefit of manipulating saturation over chroma in an artistic image-processing pipeline : the gamut represented in lightness-chroma space has a narrow, pointy end near black. As a result, increasing chroma in the lower gamut cone has an high probability of pushing colours outside of the gamut boundary. But since the saturation is the chroma divided by the brightness, the representation of the gamut in brightness-saturation space shows an asymptotic behaviour near black, and on the whole lower gamut cone for that matter. This makes the saturation more uniform (closer to a cylinder than a cone) over the brightness axis and thus the saturation control is more even too, reducing the risk of pushing valid colours out of the gamut.
#Painter’s saturation
Though the saturation-brightness model is an nice improvement over the classical chroma-lightness, it still doesn’t achieve our initial goal : degrading primaries into pastels, and finally into white. For this, we will need some rotations and distortions of the saturation-brightness space.
Let us start with $W$, that could be called “whiteness”. Using an additive light framework, whiteness will be maximal for highly emissive colours, that is white and RGB primaries (or even monochromatic lights from the boundary of the visible locus. Therefore:
$$ W = \sqrt{(1 - B)^2 + S^2} $$
So we can create a $(W, S)$ space. However, the graph will only occupy the $± \pi / 4$ angular sector around the $W$ axis, so we also need to open this angle. Using polar coordinates, we can force a rotation of the $S$ axis to create the $(W’, S’)$ space such that:
$$ \begin{align} r &= \sqrt{W^2 + S^2} = \sqrt{W’^2 + S’^2} \\ \gamma &= \arctan2(W, S) \\ \theta &= \dfrac{\gamma - \pi / 4}{\pi / 2 - \pi / 4} \cdot \pi / 2 \\ W’ & = r \cos(\theta)\\ S’ &= r \sin(\theta) \end{align} $$
The reverse model yields:
$$ \begin{align} \theta &= \arctan2(W’, S’) \\ \gamma &= \dfrac{\theta}{\pi / 2} \cdot \left(\frac{\pi}{2} - \frac{\pi}{4}\right) + \frac{\pi}{4}\\ S &= \sqrt{\dfrac{r^2}{1 + \tan(\gamma)^2}} \\ W &= \sqrt{r^2 - S^2}\\ B &= 1 \pm \sqrt{W^2 - S^2} \end{align} $$
Now, the sRGB gamut appears as follow (grey represents colours within the visible locus but outside of sRGB gamut):



On the vertical axis, all achromatic colours are near-white, so moving colours along the horizontal direction indeed degrades toward pastels or primaries. Moving colours along the vertical direction makes colours more or less emmisive.
#Flatening the model and planning for gamut mapping
#Reformulation of hypotheses and models
We have now a fairly accurate model that allows us to achieve the inital goal : writing a colour transform that degrades primary colours trough pastels into white, and the other way around, in a smooth way and with a simple linear operation. But such operations can and will push valid colours out of the working RGB space gamut, so we need a safety measure to prevent that.
If we summarize the work done so far, we have :
- mapped radiometric luminance to lightness $L^*$ using Munsell value,
- distorted the CIE 1931 xy chromaticities to create an uniform $(U, V)$ chromaticity space,
- expressed the Munsell chroma in terms of $(U, V)$ coordinates and lightness $L^*$,
- discovered that the $(U, V)$ space was not hue-linear and that the angle with achromatic locus $\theta = \arctan(V / U)$ was a poor estimate of Munsell hue,
- created an $(U’, V’)$ space based on the polar coordinates chroma and $\theta$,
- distorted the $(U’, V’)$ space non-linearily and non-uniformingly to create a new $(U’’, V’’)$ where $\arctan(V’’ / U’’)$ is indeed an accurate correlate of Munsell hue,
- discovered that the radius $\sqrt{U’’^2 + V’’^2}$ was then a poor and non-uniform metric of the chroma correlate,
- re-expressed Munsell chroma in terms of $(U’’, V’’)$ with computationnaly-expensive function using several transcendent and power functions
Then, fitting brightness to account for the Helmholtz-Kohlrausch effect, we discovered that it is fairly independent from hue but really sensitive to the accuracy of the chroma fitting.
Looking back at the sRGB gamut represented in Oklab lightness-chroma space, we notice that the lower gamut cone has a straight shape. This is desirable for the gamut-mapping feature : the lower gamut boundary can be expressed as a simple ratio of the gamut cusp chroma with its lightness. For a given hue, this ratio will be enough to describe analytically the boundary locus, and we only need a hue-wise LUT to record that ratio.
In the meantime, our model is cumbersome, with 2 different chroma estimates and 3 different UCS variants depending on the desired space properties. The initial goal of using MacAdam moments formalism for saturation and brightness failed at the inversion stage, which makes this constraint unnecessary after all.
This goal of a straight lower gamut boundary can be achieved only by fitting both chroma and lightness. We see on the $C’$ refined estimate that the gamut boundary is indeed straighter than the initial estimate $C$. The $C$ estimate is expressed from the colorfulness $M$ (which is the simple radial distance from achromatic locus in $(U, V)$ space) and $L^*$ itself.
The Munsell renotation of 194325 does not try to equate the scale of the value axis with the scale of the chroma axis, so the delta E is non-uniform across axes. I found out that compressing the Munsell chroma renotation by a factor before doing the 2D chromaticity fitting helped with hue linearity. The optimal factor was found as a part of the fitting to be approximately 123. This discrepancy along axes is of no consequence for the saturation-brightness estimate since Helmholtz-Kohlrausch brightness is explicitely fitted later from both lightness and chroma, and the model will properly reweigh chroma accordingly to lightness.
In this stage, I use the extrapolated Munsell colours from Judd & Wyszecki26, which add more samples, albeit synthetic, for Munsell values below 1. This is important because the dark region is under-constrained otherwise, and the lightness matching function can take too many forms otherwise. Only the extrapolated colours having strictly positive CIE XYZ 1931 coordinates were kept.
#New fittings
The flattened and simplified comprehensive model proposed is:
$$ \begin{align} U &= \dfrac{\alpha x + \beta y + \gamma}{D} \\ V &= \dfrac{\delta x + \epsilon y + \zeta}{D} \\ D & = \eta x + \theta y + \iota \\ U^* &= sign(U) \dfrac{\kappa |U|}{|U| + \mu} \\ V^* &= sign(V) \dfrac{\nu |V|}{|V| + \omicron} \\ \begin{bmatrix} U^{*’} \\ V^{*’} \end{bmatrix} &= [A] \cdot \begin{bmatrix} U^* \\ V^* \end{bmatrix}\\ H &= \arctan(V^{*’} / U^{*’}) \\ M &= \sqrt{U^{*’} + V^{*’}} \\ L^* &= \dfrac{\tau Y^\upsilon}{Y^\upsilon + \phi} \\ C &= \omega \cdot \left(L^* \left(\frac{M}{L^*}\right)^\chi \right)^\psi \\ J &= \left(\dfrac{L^*}{L^*_{white}}\right)^{cz} \end{align}$$
The $(L^*, C, H)$ output of the model is fitted in one single optimization against Munsell value, chroma and hue. Notice that the $(U^*, V^*)$ is an implicit cone eigenspace that will be found by the optimization rather than by explicit color matching and cone response functions. The reason for this is the CIE 1931 2° observer CMF are well-known for underestimating wavelengths below 460 nm and Judd corrected them in 195127. This problem has been reported by Sony to create perceptible white balance issues between wide-gamut OLED displays and legacy CRT displays28. Nevertheless, the whole digital imaging pipeline and the display calibration relies on the CIE 1931 observer which makes it a non-optional basis for any colour work as of 2022. But knowing the intrinsic inaccuracy of this observer makes it useless to even try to derivate explicit relationships from physiological behaviour models.
Since the Munsell dataset is based on artistic grounds rather than physiological ones, it is not necessarily aligned with the cone space principal directions. The $[A]$ matrix will allow to rotate and distort the cone eigenspace in a way that correlates with Munsell data whitout having to force the alignment of the cone eigenvectors themselves.
At the next step, the Helmholtz-Kohlrausch brightness will be modelled by:
$$B = J \times (a C^b + 1)$$
I believe that proper relative scaling of the lightness $J$ and chroma $C$, leading to uniform delta E along both axes, should be achieved when $a = 1$. Therefore, the parameter $\omega$ is retro-fitted to match that criterion after fitting the brightness.
The full optimization for chroma and value converged in more than 26 hours on Intel Xeon, due to the joint estimation of the best chroma compression factor that required around 2.302.000 iterations. The resulting model is:
$$ \begin{align} U &= \dfrac{-0.783941002840055 x + 0.277512987809202 y + 0.153836578598858}{D} \\ V &= \dfrac{ 0.745273540913283 x - 0.205375866083878 y - 0.165478376301988}{D} \\ D & = 0.318707282433486 x + 2.16743692732158 y + 0.291320554395942 \\ U^* &= sign(U) \dfrac{1.39656225667 |U|}{|U| + 1.49217352929} \\ V^* &= sign(V) \dfrac{1.4513954287 |V|}{|V| + 1.52488637914} \\ \begin{bmatrix} U^{*’} \\ V^{*’} \end{bmatrix} &= \begin{bmatrix} -1.124983854323892 & -0.980483721769325 \\ 1.86323315098672 & 1.971853092390862 \end{bmatrix} \cdot \begin{bmatrix} U^* \\ V^* \end{bmatrix}\\ H &= \arctan(V^{*’} / U^{*’}) \\ M^2 &= U^{*’} + V^{*’} \\ L^* &= \dfrac{2.098883786377 Y^{0.631651345306265}}{Y^{0.631651345306265} + 1.12426773749357} \\ C &= \dfrac{15.932993652962535}{L_{white}} \cdot (L^*)^{0.6523997524738018} (M^2)^{0.6007557017508491} \\ J &= \left(\dfrac{L^*}{L^*_{white}}\right)^{cz} \end{align}$$
The UCS per-se, allowing to compute a colour difference and presenting an uniform delta E will be composed of $L^*$ or $J$ and of opponent coordinates $u = C \cos(H)$, $v = C \sin(H)$. A such space is of no use for the present application, except for the chromaticity diagram below, so we only use $B$ or $J$, $S$ or $C$ and $H$ from now on.
The correlates are better than before:
The 1D chroma correlate is on-par with the refined $C’$ above (R² = 0.96 instead of 0.97) but the angular hue error is worse than the refined hue $H$ above (RMSE = 0.0338 instead of 0.0302). However, the chromaticity diagram shows straight lines for Munsell hues in the blue region, the most pathological one, and curved hue lines appear in the green region, the least pathological. As far as artistic colour changes are concerned, this might be good enough.
The graphs above reproduce a similar view to the Munsell pages of constant hues. Recomputing the saturation error ($6.86 C / J$ compared to $\frac{\text{Munsell chroma} / 20}{\text{Munsell value} / 10}$), we get a cumulative RMSE of 0.23, compared to 0.35 in the initial fitting and 1.20 for Oklab. Note that the $C$ upscaling is necessary here because we downscaled it in the model in order to get even delta E scaling on chroma and lightness. It also comes at no surprise that the euclidean distance from the achromatic locus is not directly a correlate of Munsell chroma, in fact all the modern CAMs (Hunt, Nayatani, CIE CAMs) scale it by a factor to get the colorfulness, and rescale the colorfulness again (possibly with a hue-wise excentricity factor) to get to the chroma.
The total hue RMSE (computed on a hue-per-hue basis, this time) is now 0.55, compared to 0.56 in the initial fitting and 0.50 for Oklab.
| Munsell hue | Oklab hue deviation | dt UCS hue deviation | Oklab saturation deviation | dt UCS saturation deviation |
|---|---|---|---|---|
| 10 RP | 0.116 | 0.104 | 0.179 | 0.026 |
| 2.5 R | 0.109 | 0.091 | 0.162 | 0.026 |
| 5 R | 0.109 | 0.087 | 0.164 | 0.030 |
| 7.5 R | 0.113 | 0.093 | 0.163 | 0.031 |
| 10 R | 0.128 | 0.108 | 0.163 | 0.029 |
| 2.5 YR | 0.111 | 0.102 | 0.130 | 0.017 |
| 5 YR | 0.081 | 0.089 | 0.100 | 0.017 |
| 7.5 YR | 0.074 | 0.079 | 0.091 | 0.020 |
| 10 YR | 0.062 | 0.079 | 0.087 | 0.023 |
| 2.5 Y | 0.045 | 0.068 | 0.082 | 0.023 |
| 5 Y | 0.044 | 0.057 | 0.078 | 0.023 |
| 7.5 Y | 0.029 | 0.030 | 0.077 | 0.020 |
| 10 Y | 0.020 | 0.014 | 0.076 | 0.018 |
| 2.5 GY | 0.026 | 0.024 | 0.075 | 0.014 |
| 5 GY | 0.047 | 0.055 | 0.084 | 0.013 |
| 7.5 GY | 0.047 | 0.059 | 0.089 | 0.014 |
| 10 GY | 0.051 | 0.067 | 0.107 | 0.014 |
| 2.5 G | 0.063 | 0.082 | 0.136 | 0.013 |
| 5 G | 0.054 | 0.075 | 0.140 | 0.019 |
| 7.5 G | 0.048 | 0.072 | 0.141 | 0.020 |
| 10 G | 0.043 | 0.074 | 0.141 | 0.029 |
| 2.5 BG | 0.050 | 0.095 | 0.136 | 0.027 |
| 5 BG | 0.058 | 0.120 | 0.121 | 0.020 |
| 7.5 BG | 0.054 | 0.126 | 0.116 | 0.013 |
| 10 BG | 0.060 | 0.141 | 0.112 | 0.011 |
| 2.5 B | 0.058 | 0.140 | 0.113 | 0.019 |
| 5 B | 0.055 | 0.139 | 0.118 | 0.031 |
| 7.5 B | 0.072 | 0.131 | 0.135 | 0.038 |
| 10 B | 0.101 | 0.104 | 0.138 | 0.043 |
| 2.5 PB | 0.118 | 0.072 | 0.158 | 0.052 |
| 5 PB | 0.148 | 0.051 | 0.186 | 0.064 |
| 7.5 PB | 0.107 | 0.097 | 0.564 | 0.131 |
| 10 PB | 0.089 | 0.063 | 0.422 | 0.065 |
| 2.5 P | 0.077 | 0.043 | 0.356 | 0.056 |
| 5 P | 0.060 | 0.032 | 0.300 | 0.039 |
| 7.5 P | 0.020 | 0.033 | 0.256 | 0.033 |
| 10 P | 0.045 | 0.062 | 0.226 | 0.032 |
| 2.5 RP | 0.069 | 0.084 | 0.210 | 0.032 |
| 5 RP | 0.097 | 0.104 | 0.196 | 0.029 |
| 7.5 RP | 0.105 | 0.103 | 0.179 | 0.023 |
| TOTAL | 0.4948 | 0.5530 | 1.20 | 0.23 |
We see here that the hue linearity favours darktable UCS for the red and purple region, but Oklab for the green and blue region. They are at a tie for the yellow region. An interesting behaviour is shows around 10 B, where they perform similarly bad : Oklab shows more than twice the hue error of darktable UCS for the purple-blue region, while darktable UCS shows more than twice the hue error of Oklab for the green-blue region, like a phase inversion. There is a high chance that this problem is linked to the under-prediction of the blue CMF in the CIE 1931 2° observer and it is likely to never be fixed as long as the digital pipeline holds onto this flawed observer, instead of moving on to CIE 2006 or 2012 observers.
Nevertheless, we traded off a bit of hue linearity for the sake of large improvement over the chroma/lightness uniformity, which is critical to traverse the hue planes in diagonal directions and to predict the Helmholtz-Kohlrausch brightness.
The new $L^*$ transform is closer to the CIE CAM16 achromatic response than the previous, so the $cz$ exponents that compensate the Stevens effect on lightness should be applicable here too for adaptation purposes :
In standard average viewing conditions, $cz = 1$ by design, so $L^* / L^*_{white} = J$ and the $cz$ exponent will have no effect on colour manipulation.
Then I refit the brightness $B$ against $JCH$ to find a very close result that improves the correlation on all datasets:
$$B = J \times (C^{1.33654221029386} + 1)$$
The brightness correlate is much improved for Sanders & Wyszecki 1963, but the Wyszecki 1967 is still offset over the identity line, although presenting a correct overall alignment. The Withouck & al. has slightly worsened and the Fairchild & Pirotta is all over the place, so the R² factor is pretty much meaningless. Since Withouck & al. is an experiment on uncorrelated colours and the Sanders & Wyszecki 1963 used correlated colours, this model might work better for natural images.
Note that, while my xyY→JCH transform is more complicated than the typical UCS, the brightness model is then amazingly simple and compact, requiring no hue-wise excentricity parameter. Simpler models (CIE Luv 1976, CIE Lab 1976, or even CIE CAM16 if we consider it simpler) yield much more complicated hand-tuning of their correlates to predict HKE (see Nayatani29 over CIE Luv, Fairchild & Pirotta for CIE Lab23, Hellwig & Fairchild20 for CIE CAM16).
Regarding the painter’s saturation, I changed the initial formulation to remove the inversion $W = 1 - B$ that would fail if the lightness, then the brightness, had not been normalized properly before. Also, the rotation is inelegant and ultimately not needed. I re-express this second order saturation with a whiteness $W$ and a purity $P$ like so :
$$ \begin{align} W &= \sqrt{S^2 + B^2}\\ P &= \frac{S}{W} \end{align} $$
#Final synthetic sweeps
I display below the sRGB gamut slices containing the sRGB primaries. In grey are displayed the visible colours outside of sRGB locus. For the JCH space, the chroma $C$ is magnified 4 times compared to the scale of the lightness $J$.




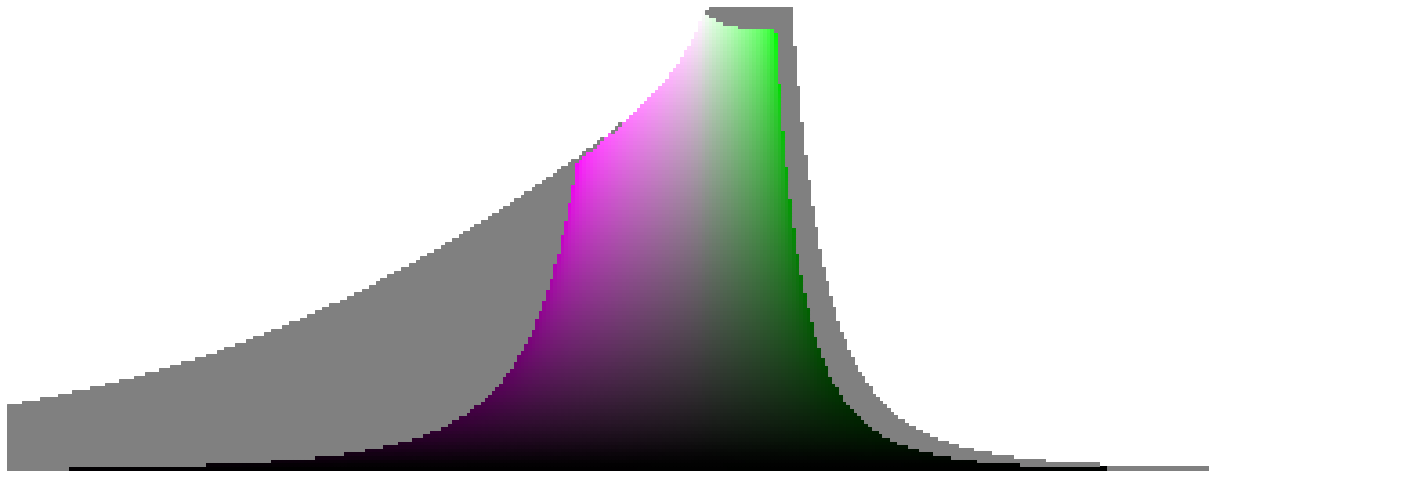




Looking at the sRGB gamut in JCH space, we get a hue linearity on-par with the second stage $(H, r)$ space above but a more even chroma distribution, and more importantly for our gamut-clipping goal : a straighter lower gamut boundary. Using large gamut spaces, we can approximate this lower bound by a simple line with a limited error.
The blue-yellow gradient shows a slight but not significant shift to purple close to achromatic. The yellow opponent of the sRGB blue looks a lot closer to the complementary colour, as shown in the first stage of optimization above. Looking at the hue angle between primaries and secondary for the sRGB space, we get :
| Blue→Yellow | Magenta→Green | Red→Cyan |
|---|---|---|
| 180.86° | 179.68° | 183.91° |
So this space can indeed be used, within a 4° hue error, for additive mix of complementary colours. More work on its connection to MacAdam moments should be done to assess the best way to make it work reliably for this application.


The correction for the Helmholtz-Kohlrausch effect is better than previously, noticeably for blues. Reds are still a bit too bright.
The continuous gradients show no outliers :



The interesting thing is there is barely any visual difference between the 3 sub-spaces above when seen against a white background (chroma setup). The next round of graphs will show a completely different behaviour when seen against grey backgrounds…
Below, we compare the effect of varying $C$, $S$ and $P$ at constant $J$, $B$ and $W$ (for all colours including the backgrounds) respectively in JCH, HSB and HPW spaces. Notice that for achromatic colors, $C = S = P = 0$ so $J = B = W$, therefore greys provide a constant reference between spaces. Hues are aligned over the vertical axis and evenly spaced. $C$, $S$ and $P$ vary along the horizontal axis.









We note that, though it improves a lot the JCH space regarding brightness uniformity, the HSB space is still subject to fluorence. The HPW space seems to only produce non-fluorent colors, that is colors that always seem non-emissive against their background. This might be a new input to characterize the greyness boundary.
#Implementation for colour grading
The implementation of the HPW space for purity artistic grading shows a poor numerical behaviour, that can be attributed to the fact that black exists on both vertical and horizontal axes ends, and the RGB gamut becomes highly concave. In practice, reducing purity from high saturation to nearly white traverses trough a large out-of-gamut region, and increasing it will make saturated colours degrade into pure black too fast.
Additionnaly, the whiteness $W = \sqrt{S^2 + B^2}$ implies that the reverse model $B = \sqrt{W^2 - S^2}$ needs to be clipped when $W^2 - S^2 < 0$, which happens a lot in natural images after artistic changes. This is simply not usable for colour grading. Changing $P$ for $S$ or even $\arctan(S, B)$ yields the same issues.
Instead of this, I propose an approach that I already used in JzAzBz in darktable 3.4 and that resembles the initial geometric color change that started this article.
The darktable UCS HSB space is desirable for its brightness, accounting for the achromatic strength (through the lightness J) and the chromatic strength (through the chroma C), and discarding the Helmholtz-Kohlrausch effect. However, the sweeps above show that grading saturation directly in HSB is not enough to prevent degrading grey colours into fluorent colours (colours that will appear as if they were fluorescent or self-emitting when evaluated against their surround). A sort of second order saturation, such that $S’ = C / B^2 = S / B$, improves this behaviour slightly in the sense that fluorence starts at higher saturation values, but still happens.
So we can use an HCB space, where $C = B \times S$ comes as-is from JCH space, and B is the brightness taken from the HSB space. The HCB space is essentially a JCH space where J is rescaled to account for HKE. In a such space, equi-saturation lines are defined by a constant ratio $C / B = S$ and are directly the diagonal lines passing through $(0, 0)$ (black locus). I show the sRGB gamut slices at constant hue in HCB space below (the $C$ axis is magnified by a factor of $10 / 3$ for clarity) :



The method is to extract the direction of the local saturation eigenvector $\vec{S}$ for each pixel, such that $||\vec{S}|| = \sqrt{C^2 + B^2}$ and $\arg(\vec{S}) = \arctan(C / B) = \sigma $. Then, we rotate the $(B, C)$ plane by an angle $\sigma$ to get the colour properties aligned on the eigenvector :
$$ \begin{bmatrix} P \\ W \end{bmatrix} = \begin{bmatrix}\cos(\sigma) & -\sin(\sigma) \\ \sin(\sigma) & \cos(\sigma)\end{bmatrix} \cdot \begin{bmatrix} C \\ B \end{bmatrix} $$
Note that, for numerical implementations, we can evaluate $\sin(\sigma)$ and $\cos(\sigma)$ directly from the euclidean coordinates, such that :
$$ \begin{align} \cos(\sigma) &= \frac{B}{\sqrt{C^2 + B^2}} \\ \sin(\sigma) & = \frac{C}{\sqrt{C^2 + B^2}} \end{align} $$
This spares us 3 evaluations of transcendent functions, one of them being the explicit evaluation of $\sigma = \arctan(C / B)$ that is not needed for this application.
Also, because $\vec{S}$ is the “colour” eigenvector, $P = 0$ for all sets of coordinates $(C, B)$, so this coordinate is void and its evaluation is pointless. Therefore, we directly initialize it with $C$ to give it a non-zero value on which we can apply a gain later.
Then, the user will define 2 factors $k$ and $l$ in $[0; 2]$ that will be used to gain the $(P, W)$ coordinates :
$$ \begin{align} P’ &= l \cdot C - C \\ W’ &= k \cdot W \end{align} $$
By subtracting $C$ straight away from $P’$, we make sure that $P’ = 0$ if $l = 1$, so the gain $k$ will be a pure rescaling along the direction of the eigenvector. $C$ is used here only as a temporary control quantity.
Then we rotate back $(P’, W’)$ to $(C, B)$ space using the invert of the initial rotation matrix:
$$ \begin{bmatrix} C \\ B \end{bmatrix} = \begin{bmatrix} \cos(\sigma) & \sin(\sigma) \\ -\sin(\sigma) & \cos(\sigma) \end{bmatrix} \cdot \begin{bmatrix}P’ \\ W’ \end{bmatrix} $$
This colour shift is equivalent to a pure rotation around the black locus (origin of $B$ and $C$ axes) for small $l$ values : it will increase the saturation and darken at the same time, more than a direct saturation change at constant brightness $B$ in HSB space. Therefore, it resembles the painter’s saturation (degrading primaries into white and the other way around), without the numerical side-effects of the previous HPW space. Using a pure rotation defined in polar coordinates here has the same shortcomings as the HPW space : gaining angles by a factor 2 will produce little displacement close to achromatic (angles < 5°), but angles larger than 45° will immediately be sent to 90°, resulting in clipping to black. This results in a deeply uneven behaviour and is difficult to control. The pseudo-rotation using the eigenvector shown here is smoother and more evenly behaved.
For achromatic colours, the $P$ dimension becomes the chroma $C$ itself. As the saturation increases, the $P$ axis plunges more and more toward black.
Unfortunately, this transform is not a space anymore, in the sense that it has no closed-form equation, is not revertible because the rotation matrix is built upon the original colours before color shift, and it is not bijective either, meaning the same final colour can be produced by shifting 2 different input colours.
#Gamut mapping
The reverse transform from darktable UCS HSB to HCB to JCH to CIE xyY 1931 yields :
$$ \begin{align} C &= S \cdot B \\ J &= \frac{B}{C^{1.33654221029386} + 1} \\ L^* &= J^{1 / cz} \cdot L_{white} \\ M &= \left(\frac{C \cdot L_{white}}{15.932993652962535 \cdot (L^*)^{0.6523997524738018}}\right)^{0.8322850678616855} \\ U^{*’} &= M \cdot \cos(H) \\ V^{*’} &= M \cdot \sin(H) \\ \begin{bmatrix} U^* \\ V^* \end{bmatrix} &= \begin{bmatrix} 5.037522385190711 & - 2.504856328185843 \\ 4.760029407436461 & 2.874012963239247 \end{bmatrix} \cdot \begin{bmatrix} U^{*’} \\ V^{*’} \end{bmatrix} \\ U &= sign(U^*) \frac{-1.49217352929 |U^*|}{|U^*| - 1.39656225667} \\ V &= sign(V^*) \frac{-1.52488637914 |V^*|}{|V^*| - 1.4513954287} \\ D &= 0.940254742367256 * U + V - 0.0256325967652889 \\ x & = \frac{0.167171472114775 \cdot U + 0.141299802443708 \cdot V - 0.00801531300850582}{D} \label{eqn-x} \\ y & = \frac{-0.150959086409163 \cdot U - 0.155185060382272 \cdot V - 0.00843312433578007}{D} \label{eqn-y} \\ Y & = \left(\frac{-1.12426773749357 L^*}{L^* - 2.098883786377}\right)^{1.5831518565279648} \end{align}$$
Allowing to manipulate colours in HCB or JCH means that there is no guaranty on the validity of $x$ and $y$ chromaticity coordinates, and there is a good chance that pushing saturation or chroma made them fall outside of our working RGB gamut. We need to sanitize them before injecting them back into our processing pipeline. Gamut-mapping straight after an artistic colour-grading is a good idea since both operations are done at constant hue, which we explicitely computed. So the gamut-mapping problem breaks down to finding the maximum chroma at current hue that fits within the working RGB space gamut.
From $\eqref{eqn-x}$ and $\eqref{eqn-x}$, we can write the algebraic constraint:
$$D > 0$$
From the construction of CIE xyY space, we can write the following validity constraints:
$$\begin{align} 0 \leq &x \leq 1 \\ 0 \leq &y \leq 1 \\ x + y &\leq 1 \end{align}$$
These constraints ensure that the resulting xyY vector lies within the visible locus. But we could go one step further and ensure they lie within the working RGB space gamut. RGB primaries are defined from CIE XYZ 1931 2° by a simple matrix, which allows us to compute the boundary of the gamut in terms of xyY chromaticity. The gamut coverage of RGB spaces has a well-known triangular shape in the xyY chromaticity graph:

But if we slice the gamut space at constant “hue” in an Ych space derivated from xyY through Yuv (using D65 illuminant as the achromatic locus), the bounds are straight too :
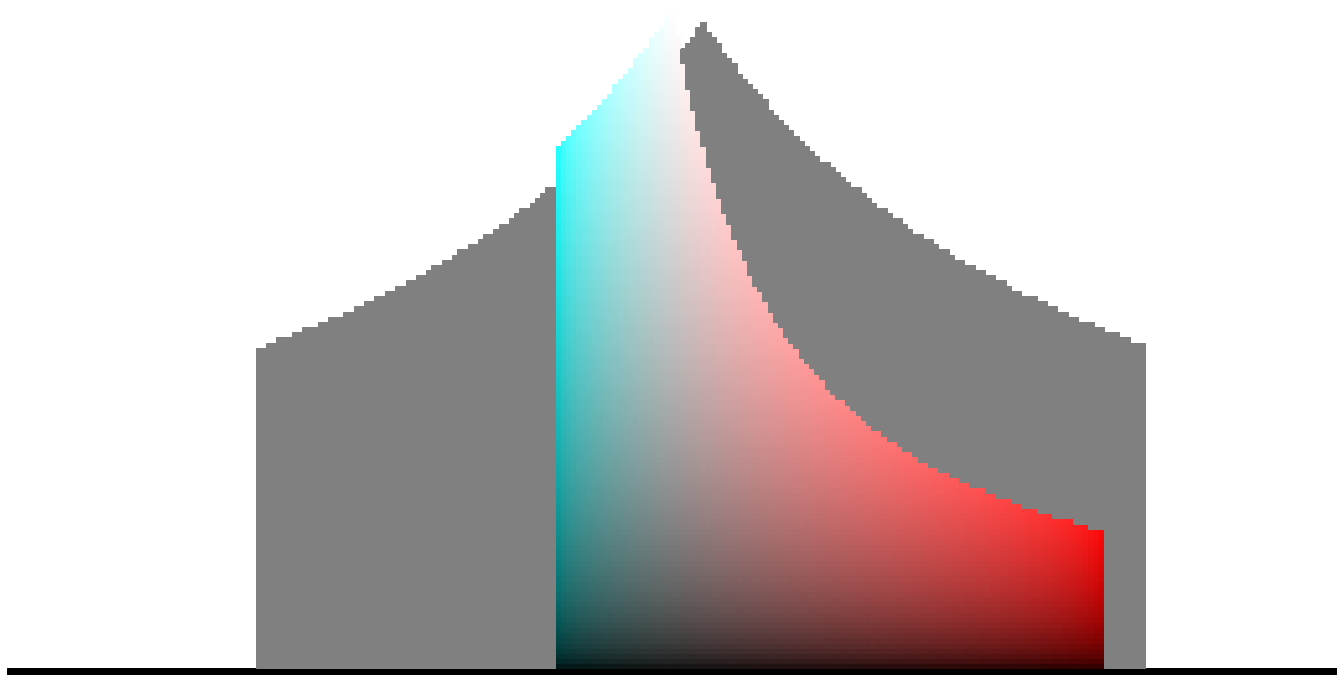


Although not all luminances allow the maximum saturation, it is already a first start toward an analytical description of the gamut boundary. Let us denote the constants $(x_R, y_R)$, $(x_G, y_G)$ and $(x_B, y_B)$ CIE xyY chromaticities of the working RGB space primaries. We can write the gamut boundary as a collection of 1D algebraic functions or equivalent 2D parametric functions:
$$\begin{align} \mathfrak{B}_1 &: y = y_B + \frac{y_R - y_B}{x_R - x_B} \cdot (x - x_B) \Leftrightarrow \begin{cases} x(t) &= x_B + t \cdot (x_R - x_B) \\ y(t) &= y_B + t \cdot (y_R - y_B) \end{cases}\\ \mathfrak{B}_2 &: y = y_R + \frac{y_G - y_R}{x_G - x_R} \cdot (x - x_R) \Leftrightarrow \begin{cases} x(t) &= x_R + t \cdot (x_G - x_R) \\ y(t) &= y_R + t \cdot (y_G - y_R) \end{cases}\\ \mathfrak{B}_3 &: y = y_G + \frac{y_B - y_G}{x_B - x_G} \cdot (x - x_G) \Leftrightarrow \begin{cases} x(t) &= x_G + t \cdot (x_B - x_G) \\ y(t) &= y_G + t \cdot (y_B - y_G) \end{cases}\\ & \forall t \in [0; 1], , (x, y) \in [0; 1]^2 \nonumber \end{align}$$
We need to rewrite those equations to express the distance between the triangular boundaries and the achromatic locus, D65 in our case. For each boundary $\mathfrak{B}_1, \mathfrak{B}_2, \mathfrak{B}_3$, this is equivalent to $r(t) = \sqrt{(x(t) - x_{D65})^2 + (y(t) - y_{D65})^2}$. This means that, to lie within the RGB locus, any set of $(x, y)$ chromaticities should validate the constraint $\sqrt{(x_{D65} - x)^2 + (y_{D65} - y)^2} \leq r(t)$. The problem then becomes how to choose which $r(t)$ function, that is which boundary, is relevant for any given set of $(x, y)$ chromaticity.
For this purpose, the $t$ silent variable needs to be connected to a meaningful parameter. Since $r(t)$ is the radial distance to achromatic, it only seems logical to map it to an angle, as to make a polar system of coordinates appear. Let us renote our xyY chromaticities as uvY, where $u = x - x_{D65}$ and $v = y - y_{D65}$. The radial distance to achromatic becomes naturally $c = \sqrt{u^2 + v^2}$ and the associated angle is $h = \arctan(v / u)$.
For each boundary between 2 vertices (defined as the RGB primaries), $t \in [0; 1]$ : $t = 0$ on the initial RGB vertice of the boundary line, and $t = 1$ on the final vertice of the boundary line. For the green→blue boundary, we get:
$$\begin{align} h &= \arctan\left(\frac{v}{u}\right) \\ \tan(h) &=\frac{v}{u} \\ \tan(h) &= \frac{y_G + t \cdot (y_B - y_G) - y_{D65}}{x_G + t \cdot (x_B - x_G) - x_{D65}} \\ t &= \frac{y_{D65} - y_G + \tan(h) \cdot (x_G - x_{D65})}{y_B - y_G + \tan(h) \cdot (x_G - x_B)} \in [0; 1] \end{align}$$
The final matter is to identify the relevant boundary for a given $(x, y)$ set. Comparing the $h$ angle directly to the angles of the RGB primaries yields to non-uniform heuristics. The following proposed test yields to uniform data handling, $\forall {h_B, h_G, h_R} \in [-\pi; \pi]$, where $h_B, h_G, h_R$ denote the angles of the RGB primaries in xyY 1931 space compared to D65 achromatic locus :
$$\begin{align} h \in \mathfrak{B}_1 \Leftrightarrow \dfrac{h - h_B}{h_R - h_B} \in [0; 1] \\ h \in \mathfrak{B}_2 \Leftrightarrow \dfrac{h - h_R}{h_G - h_R} \in [0; 1] \\ h \in \mathfrak{B}_3 \Leftrightarrow \dfrac{h - h_G}{h_B - h_G} \in [0; 1] \end{align}$$
Only one of those condition holds true at a time, except for chromaticities located on the vertices exactly. Now, the problem we face is the numerical scaling of the angles, since $0 \equiv 2 \pi$ and $-\pi \equiv \pi$. To take care of this in a way that preserves the sign of angles, assuming the $h$ angle was obtained through an atan2 function outputing angles in $[-\pi; \pi]$ (as C-based languages do), each difference of angles needs to be corrected like this :
$$\Delta H(h_1, h_2) = \begin{cases} h_1 - h_2 + 2 \pi & \text{ if } & h_1 - h_2 < - \pi \\ h_1 - h_2 - 2 \pi & \text{ if } & h_1 - h_2 > \pi \\ h_1 - h_2 & \text{else} & \end{cases}$$
Preserving the sign of the difference of angles will ensure that the ratios will always be in $[0; 1]$ when the boundary is relevant for the current test set $(x, y)$.
Below, I draw the predicted gamut boundary for the sRGB space using the above equations for $x(t)$ and $y(t)$. The parameter $t$ is computed by varying $h$ in $[-\pi; \pi]$. The projected distance to achromatic uses the parametric equation :
$$\begin{cases} x_r(t) &= r(t) \cdot \cos(h) + x_{D65}\\ y_r(t) &= r(t) \cdot \sin(h) + y_{D65} \end{cases}$$

The maximum numerical absolute error between the boundary locus expressed directly from $(x(t), y(t))$ and the projected distance to achromatic $r(t)$ is $8 \cdot 10^{-16}$ and located near $\pi \pm 0.2 \pi$.
The complete algorithm checking that any colour of chromaticity $(x, y)$ in CIE xyY 1931 2° space lies within $\Gamma_{RGB}$ the gamut of the working RGB space, goes as follow :
$$\begin{align} u & = x - x_{D65} \\ v & = y - y_{D65} \\ c & = \sqrt{u^2 + v^2} \\ h & = \arctan2(v, u) \\ \mathfrak{B}(h) & = \begin{cases} \mathfrak{B}_1 &\text{if}& 0 \leq \dfrac{\Delta H(h, h_B)}{\Delta H(h_R, h_B)} < 1 \\ \mathfrak{B}_2 &\text{if}& 0 \leq \dfrac{\Delta H(h, h_R)}{\Delta H(h_G, h_R)} < 1 \\ \mathfrak{B}_3 &\text{if}& 0 \leq \dfrac{\Delta H(h, h_G)}{\Delta H(h_B, h_G)} < 1 \end{cases}\\ \text{if} , \mathfrak{B}(h) = \mathfrak{B}_1 &: \begin{cases} t & = \dfrac{y_{D65} - y_B + \tan(h) \cdot (x_B - x_{D65})}{y_R - y_B + \tan(h) \cdot (x_B - x_R)} \\ x(t) &= x_B + t \cdot (x_R - x_B) \\ y(t) &= y_B + t \cdot (y_R - y_B) \end{cases} \\ \text{if} , \mathfrak{B}(h) = \mathfrak{B}_2 &: \begin{cases} t & = \dfrac{y_{D65} - y_R + \tan(h) \cdot (x_R - x_{D65})}{y_G - y_R + \tan(h) \cdot (x_R - x_G)} \\ x(t) &= x_R + t \cdot (x_G - x_R) \\ y(t) &= y_R + t \cdot (y_G - y_R) \end{cases} \\ \text{if} , \mathfrak{B}(h) = \mathfrak{B}_3 &: \begin{cases} t & = \dfrac{y_{D65} - y_G + \tan(h) \cdot (x_G - x_{D65})}{y_B - y_G + \tan(h) \cdot (x_G - x_B)} \\ x(t) &= x_G + t \cdot (x_B - x_G) \\ y(t) &= y_G + t \cdot (y_B - y_G) \end{cases} \\ r(t) &= \sqrt{(x(t) - x_{D65})^2 + (y(t) - y_{D65})^2}\\ \text{result} &: \begin{cases} (x, y) \in \Gamma_{RGB} & \text{if} & c \leq r(t) \\ (x, y) \notin \Gamma_{RGB} & \text{else} \\ \end{cases} \end{align}$$
Now, this is only mildly relevant for our application, first because the angle on the xy plane does not display a constant perceptual hue (Abney effect), then because we need a representation of the gamut inside our UCS to avoid back-and-forth transforms as well as to allow gamut-mapping at constant brightness (taking HKE into account).
It is easy to inject the parametric equations of the gamut boundaries $x(t)$ and $y(t)$ in place of $x$ and $y$ into the xyY→dt UCS transform. Although the shape of the equations looks daunting, expressing the gamut boundary as the maximum colorfulness $M$ (radial distance to achromatic) is not too difficult. However, it will not be possible to formulate the parameter $t$ in a way that allows it to be connected to the perceptual hue $H$, because the transform uses an absolute value that prevents inversion, so the equation $V^{*'}(t) / U^{*'}(t) = \tan(H)$ cannot be solved for $t$.
The solution is therefore to march the gamut boundary in CIE xyY 1931, for $h$ varying in $[-\pi; \pi[$, then convert $x(t)$ and $y(t)$ to the UCS $U^{*'}$ and $V^{*'}$ coordinates, then record the perceptual hue $H$ and the colorfulness $M = \sqrt{U^{*'2} + V^{*'2}}$. $M$ is then stored in a look-up table (LUT) where the index corresponds to the hue $H$ discretized by steps of 1°. The Python program to build the LUT for any RGB space is given below, in the source code section, along with a pre-computed LUT for sRGB. This makes for an efficient LUT construction at runtime, because we don’t need to sweep over the full volume.

For each pixel expressed in JCH, from the LUT of maximum colorfulness $M_{max}$ at the current $H$, we can compute the maximum chroma $C_{max}$ at the lightness of the pixel $J$. From there, we can compute the maximum brightness $B_{max}$ with $C_{max}$ and $J$, and finally the maximum saturation $S_{max} = C_{max} / B_{max}$. With the pixel expressed in HSB, we can clip $S$ to $S_{max}$ at constant brightness, and go back to JCH, then xyY, then finally RGB.
Follow the development and grab the code on Colab : https://drive.google.com/file/d/1kPAH7If70XdmrxmMcE_EQNitMppfsIns/view?usp=sharing
#Source code
#Python
1# Copyright 2022 - Aurélien PIERRE / darktable project
2# URL : https://eng.aurelienpierre.com/2022/02/color-saturation-control-for-the-21th-century/
3# The following source code is released under the MIT license
4# (https://opensource.org/licenses/MIT) with the following addenda :
5# * Any reuse of this code shall include the names of the author and of the project, as well as the source URL,
6# * Any implementation of this colour space MUST call it "darktable Uniform Color Space" or
7# "darktable UCS" in the end-user interface of the software.
8
9import numpy as np
10
11def Y_to_dt_UCS_L_star(Y:np.array):
12 Y_hat = Y**0.631651345306265
13 L_star = 2.098883786377 * Y_hat / (Y_hat + 1.12426773749357)
14 return L_star
15
16
17def dt_UCS_L_star_to_Y(L_star:np.array):
18 Y = (-1.12426773749357* L_star / (L_star - 2.098883786377))**1.5831518565279648
19 return Y
20
21
22def dt_UCS_xy_to_UV(xy):
23 x = xy[:, 0]
24 y = xy[:, 1]
25
26 # The following can be vectorized with a 4×float Fused Multiply-Add
27 U = -0.783941002840055 * x + 0.277512987809202 * y + 0.153836578598858
28 V = 0.745273540913283 * x - 0.205375866083878 * y - 0.165478376301988
29 D = 0.318707282433486 * x + 2.16743692732158 * y + 0.291320554395942
30
31 U /= D
32 V /= D
33
34 U_star = 1.39656225667 * U / (np.abs(U) + 1.49217352929)
35 V_star = 1.4513954287 * V / (np.abs(V) + 1.52488637914)
36
37 # The following is equivalent to a 2D matrix product
38 U_star_prime = -1.124983854323892 * U_star - 0.980483721769325 * V_star
39 V_star_prime = 1.86323315098672 * U_star + 1.971853092390862 * V_star
40
41 return U_star_prime, V_star_prime
42
43
44def xyY_to_dt_UCS_JCH(xyY:np.array, Y_white:float = 1., cz:float = 1):
45 """
46 input :
47 * xyY in normalized CIE XYZ for the 2° 1931 observer adapted for D65
48 * L_white the lightness of white as dt UCS L* lightness.
49 * cz : c * z
50 * n = ratio of background luminance and the luminance of white,
51 * z = 1 + sqrt(n)
52 * c = 0.69 for average surround lighting
53 0.59 for dim surround lighting (sRGB standard)
54 0.525 for dark surround lighting
55 * cz = 1 for standard pre-print proofing conditions with average surround and n = 20 %
56 (background = middle grey, white = perfect diffuse white)
57 range : xy in [0; 1], Y normalized for perfect diffuse white = 1
58 """
59
60 L_star = Y_to_dt_UCS_L_star(xyY[:, 2])
61 L_white = Y_to_dt_UCS_L_star(Y_white)
62
63 U_star_prime, V_star_prime = dt_UCS_xy_to_UV(xyY)
64 M2 = U_star_prime**2 + V_star_prime**2
65 C = 15.932993652962535 * L_star**0.6523997524738018 * M2**0.6007557017508491 / L_white
66
67 J = (L_star / L_white)**cz
68 H = np.arctan2(V_star_prime, U_star_prime)
69
70 return np.vstack([J, C, H]).T
71
72
73def dt_UCS_JCH_to_xyY(JCH: np.array, Y_white:float = 1., cz:float = 1):
74 """
75 output : xyY in normalized CIE XYZ for the 2° 1931 observer adapted for D65
76 range : xy in [0; 1], Y normalized for perfect diffuse white = 1
77 """
78 J = JCH[:, 0]
79 C = JCH[:, 1]
80 H = JCH[:, 2]
81
82 L_white = Y_to_dt_UCS_L_star(Y_white)
83 L_star = J**(1 / cz) * L_white
84
85 M = (C * L_white/ (15.932993652962535 * L_star**0.6523997524738018))**0.8322850678616855
86
87 U_star_prime = M * np.cos(H)
88 V_star_prime = M * np.sin(H)
89
90 # The following is equivalent to a 2D matrix product
91 U_star = -5.037522385190711 * U_star_prime - 2.504856328185843 * V_star_prime
92 V_star = 4.760029407436461 * U_star_prime + 2.874012963239247 * V_star_prime
93
94 U = -1.49217352929 * U_star / (np.abs(U_star) - 1.39656225667)
95 V = -1.52488637914 * V_star / (np.abs(V_star) - 1.4513954287)
96
97 # The following can be vectorized with a 4×float SSE2 vector
98 x = ( 0.167171472114775 * U + 0.141299802443708 * V - 0.00801531300850582)
99 y = (-0.150959086409163 * U - 0.155185060382272 * V - 0.00843312433578007)
100 D = ( 0.940254742367256 * U + V - 0.0256325967652889)
101
102 x /= D
103 y /= D
104
105 Y = dt_UCS_L_star_to_Y(L_star)
106
107 return np.vstack([x, y, Y]).T
108
109
110def dt_UCS_JCH_to_HCB(JCH: np.array):
111 J = JCH[:, 0]
112 C = JCH[:, 1]
113 H = JCH[:, 2]
114
115 B = J * (C**1.33654221029386 + 1)
116
117 return np.vstack([H, C, B]).T
118
119
120def dt_UCS_HCB_to_JCH(HCB: np.array):
121 H = HCB[:, 0]
122 C = HCB[:, 1]
123 B = HCB[:, 2]
124
125 J = B / (C**1.33654221029386 + 1)
126
127 return np.vstack([J, C, H]).T
128
129
130def dt_UCS_JCH_to_HSB(JCH: np.array):
131 J = JCH[:, 0]
132 C = JCH[:, 1]
133 H = JCH[:, 2]
134
135 B = J * (C**1.33654221029386 + 1)
136 S = C / B
137
138 return np.vstack([H, S, B]).T
139
140
141def dt_UCS_HSB_to_JCH(HSB: np.array):
142 H = HSB[:, 0]
143 S = HSB[:, 1]
144 B = HSB[:, 2]
145
146 C = S * B
147 J = B / (C**1.33654221029386 + 1)
148
149 return np.vstack([J, C, H]).T
150
151
152def dt_UCS_HSB_to_HPW(HSB: np.array):
153 H = HSB[:, 0]
154 S = HSB[:, 1]
155 B = HSB[:, 2]
156
157 W = (S**2 + B**2)**(1 / 2)
158 P = (S / W)
159
160 return np.vstack([H, P, W]).T
161
162
163def dt_UCS_HPW_to_HSB(HPW: np.array):
164 H = HPW[:, 0]
165 P = HPW[:, 1]
166 W = HPW[:, 2]
167
168 S = W * P
169 B = W
170
171 return np.vstack([H, S, B]).T
172
173
174def dt_UCS_HSB_to_HPW(HSB: np.array):
175 H = HSB[:, 0]
176 S = HSB[:, 1]
177 B = HSB[:, 2]
178
179 W = B
180 P = W / B
181
182 return np.vstack([H, P, W]).T
183
184
185def dt_UCS_HPW_to_HSB(HPW: np.array):
186 H = HPW[:, 0]
187 P = HPW[:, 1]
188 W = HPW[:, 2]
189
190 S = P
191 B = (W**2 - S**2)**0.5
192
193 return np.vstack([H, S, B]).T
194
195
196def dt_UCS_HCB_to_HPW_cc(HCB: np.array):
197 H = HCB[:, 0]
198 C = HCB[:, 1]
199 B = HCB[:, 2]
200
201 W = (2 * C**2 + B**2)**(1 / 2)
202 P = 2 * C / W
203
204 return np.vstack([H, P, W]).T
205
206
207def dt_UCS_HPW_cc_to_HCB(HPW: np.array):
208 H = HPW[:, 0]
209 P = HPW[:, 1]
210 W = HPW[:, 2]
211
212 C = P * W / 2
213 B = (W**2 - 2 * C**2)**0.5
214
215 return np.vstack([H, C, B]).TThe precomputed LUT of the sRGB gamut boundary, expressed as the maximum colorfulness ($M$) for each integer hue angle ± 0.005° ($H$ from JCH space) between -180° and +179° (360 increments of 1°), is given below :
1sRGB_max_colorfulness =
2array([ 0.01103283, 0.01096559, 0.01090244, 0.01084332, 0.01078809,
3 0.01073671, 0.01068902, 0.01064501, 0.01060461, 0.0105677 ,
4 0.01053427, 0.01050422, 0.01047753, 0.01045418, 0.0104341 ,
5 0.01041726, 0.01040365, 0.01039325, 0.01038603, 0.01038199,
6 0.01038111, 0.01038341, 0.01038887, 0.01039752, 0.01040936,
7 0.01042441, 0.01044271, 0.01046425, 0.01048909, 0.01051726,
8 0.01054881, 0.0105838 , 0.0106223 , 0.01066431, 0.01070998,
9 0.01075928, 0.01081239, 0.01086931, 0.01093024, 0.01099525,
10 0.01106442, 0.01113783, 0.01121576, 0.01129823, 0.0113853 ,
11 0.01147735, 0.01157452, 0.01167695, 0.01178479, 0.01189835,
12 0.01201764, 0.0121434 , 0.01227548, 0.01241406, 0.01256006,
13 0.01271332, 0.01287437, 0.01304352, 0.01322141, 0.01340812,
14 0.0136047 , 0.01381129, 0.01402838, 0.01425727, 0.01449822,
15 0.01475187, 0.01501939, 0.01530113, 0.01559894, 0.01591334,
16 0.01624596, 0.01659807, 0.01697102, 0.01736703, 0.01778713,
17 0.01823393, 0.0187096 , 0.01921654, 0.0197584 , 0.02033838,
18 0.02096007, 0.02162754, 0.02234665, 0.02312297, 0.02396283,
19 0.0248752 , 0.02586723, 0.02695083, 0.02814031, 0.02944853,
20 0.03089547, 0.0325058 , 0.03430409, 0.03632699, 0.0386212 ,
21 0.04124274, 0.04426925, 0.04780478, 0.0519781 , 0.05700699,
22 0.05910492, 0.05788727, 0.05673328, 0.05563778, 0.05459784,
23 0.0536077 , 0.05266812, 0.05177262, 0.05092078, 0.0501096 ,
24 0.0493364 , 0.04859986, 0.0478986 , 0.04722956, 0.04659097,
25 0.04598273, 0.04540242, 0.0448293 , 0.04417159, 0.04343099,
26 0.04262117, 0.0417591 , 0.04089199, 0.04007221, 0.03929827,
27 0.03856648, 0.03787432, 0.0372181 , 0.03659709, 0.0360081 ,
28 0.03544889, 0.03491846, 0.03441484, 0.03393626, 0.03348194,
29 0.03304994, 0.03263926, 0.03224896, 0.03187814, 0.03152566,
30 0.03119075, 0.0308727 , 0.0305708 , 0.03028417, 0.03001245,
31 0.02975484, 0.02951099, 0.0292802 , 0.02906201, 0.02885627,
32 0.02866237, 0.02848003, 0.02830872, 0.02814842, 0.02799856,
33 0.02785909, 0.02772968, 0.02761005, 0.02750005, 0.02739951,
34 0.02730829, 0.02722612, 0.02715295, 0.02708864, 0.02703308,
35 0.02698619, 0.02694791, 0.02691814, 0.02689687, 0.02688403,
36 0.02687963, 0.02688365, 0.02689609, 0.02691698, 0.02694636,
37 0.02698427, 0.02703076, 0.02708594, 0.02714989, 0.02722269,
38 0.02730444, 0.02739533, 0.02749549, 0.02760517, 0.02772436,
39 0.02785347, 0.0279926 , 0.02814213, 0.02830214, 0.02847307,
40 0.02865512, 0.02884877, 0.02905426, 0.02927215, 0.02950267,
41 0.02974644, 0.03000394, 0.03027542, 0.03056211, 0.03086383,
42 0.03053059, 0.0290978 , 0.02784185, 0.02672645, 0.02572739,
43 0.02482429, 0.02400313, 0.02325285, 0.02256343, 0.02192813,
44 0.02134 , 0.02079409, 0.02028607, 0.01981263, 0.01936937,
45 0.01895428, 0.01856508, 0.01819887, 0.01785471, 0.01753011,
46 0.01722402, 0.01693508, 0.01666205, 0.01640413, 0.01615962,
47 0.01592854, 0.01570936, 0.01550188, 0.01530532, 0.01511895,
48 0.01494213, 0.01477475, 0.01461598, 0.01446552, 0.01432309,
49 0.01418842, 0.01406084, 0.01394016, 0.01382637, 0.01371889,
50 0.01361773, 0.01352241, 0.01343293, 0.01334902, 0.01327055,
51 0.0131974 , 0.01312934, 0.01306627, 0.01300801, 0.01295457,
52 0.01290579, 0.01286159, 0.01282185, 0.01278657, 0.01275559,
53 0.01272894, 0.01270655, 0.01268837, 0.01267434, 0.01266448,
54 0.01265876, 0.01265716, 0.01265969, 0.01266634, 0.01267712,
55 0.01269205, 0.01271119, 0.01273452, 0.0127621 , 0.01279396,
56 0.01283021, 0.01287088, 0.01291604, 0.01296573, 0.0130201 ,
57 0.0130792 , 0.01314323, 0.01321227, 0.01328628, 0.01336573,
58 0.01345047, 0.01354088, 0.01363694, 0.01373909, 0.01384731,
59 0.01396209, 0.01408344, 0.0142117 , 0.01434708, 0.01449017,
60 0.01464122, 0.01480027, 0.01496825, 0.01514523, 0.01533177,
61 0.01552847, 0.01573597, 0.01595227, 0.0161667 , 0.01637702,
62 0.01658169, 0.01677921, 0.01697564, 0.01718072, 0.01739509,
63 0.0176191 , 0.01785332, 0.01809818, 0.01835435, 0.01862179,
64 0.01890154, 0.01919387, 0.01949968, 0.01981963, 0.02015414,
65 0.02050432, 0.02087071, 0.02125426, 0.02165597, 0.02132008,
66 0.02067385, 0.02007156, 0.01950962, 0.01898366, 0.01849131,
67 0.01802902, 0.01759462, 0.01718583, 0.01680059, 0.01643727,
68 0.01609434, 0.01577 , 0.0154632 , 0.01517259, 0.01489725,
69 0.01463617, 0.01438826, 0.01415308, 0.01392951, 0.01371717,
70 0.0135152 , 0.01332305, 0.0131404 , 0.01296653, 0.01280099,
71 0.01264354, 0.01249367, 0.01235102, 0.01221531, 0.01208616,
72 0.01196335, 0.01184662, 0.01173571, 0.0116303 , 0.0115303 ,
73 0.01143549, 0.01134566, 0.01126061, 0.01118024, 0.01110434])In the above LUT, the index of the cells represents the hue angle in JCH space, and the content of the cells is the maximum colorfulness. To probe the boundary of the gamut at the current hue as the distance to achromatic, the method is :
To build the gamut boundary LUT for any RGB colour space, the procedure is the following :
1import numpy as np
2import colour
3
4def Delta_H(h_1, h_2):
5 diff = h_1 - h_2
6 diff += 2 * np.pi if diff < -np.pi else 0
7 diff -= 2 * np.pi if diff > np.pi else 0
8 return diff
9
10H = np.linspace(-np.pi, np.pi, 360 * 50)
11D65_xyY = np.array([ 0.3127, 0.329 , 1. ])
12
13# Express the RGB primaries in CIE xyY - example here with sRGB
14xyY_red = colour.XYZ_to_xyY(colour.sRGB_to_XYZ([1, 0, 0]))
15xyY_green = colour.XYZ_to_xyY(colour.sRGB_to_XYZ([0, 1, 0]))
16xyY_blue = colour.XYZ_to_xyY(colour.sRGB_to_XYZ([0, 0, 1]))
17
18# Get the "hue" angles of the primaries in xy space compared to D65
19h_red = np.arctan2(xyY_red[1] - D65_xyY[1], xyY_red[0] - D65_xyY[0])
20h_green = np.arctan2(xyY_green[1] - D65_xyY[1], xyY_green[0] - D65_xyY[0])
21h_blue = np.arctan2(xyY_blue[1] - D65_xyY[1], xyY_blue[0] - D65_xyY[0])
22
23LUT = np.zeros(360)
24
25# March the gamut boundary in CIE xyY 1931
26for angle in H:
27 t_1 = Delta_H(angle, h_blue) / Delta_H(h_red, h_blue)
28 t_2 = Delta_H(angle, h_red) / Delta_H(h_green, h_red)
29 t_3 = Delta_H(angle, h_green) / Delta_H(h_blue, h_green)
30
31 if(t_1 == np.clip(t_1, 0, 1)):
32 t = (D65_xyY[1] - xyY_blue[1] + np.tan(angle) * (xyY_blue[0] - D65_xyY[0])) / (xyY_red[1] - xyY_blue[1] + np.tan(angle) * (xyY_blue[0] - xyY_red[0]))
33 x_t = xyY_blue[0] + t * (xyY_red[0] - xyY_blue[0])
34 y_t = xyY_blue[1] + t * (xyY_red[1] - xyY_blue[1])
35 elif(t_2 == np.clip(t_2, 0, 1)):
36 t = (D65_xyY[1] - xyY_red[1] + np.tan(angle) * (xyY_red[0] - D65_xyY[0])) / (xyY_green[1] - xyY_red[1] + np.tan(angle) * (xyY_red[0] - xyY_green[0]))
37 x_t = xyY_red[0] + t * (xyY_green[0] - xyY_red[0])
38 y_t = xyY_red[1] + t * (xyY_green[1] - xyY_red[1])
39 elif(t_3 == np.clip(t_3, 0, 1)):
40 t = (D65_xyY[1] - xyY_green[1] + np.tan(angle) * (xyY_green[0] - D65_xyY[0])) / (xyY_blue[1] - xyY_green[1] + np.tan(angle) * (xyY_green[0] - xyY_blue[0]))
41 x_t = xyY_green[0] + t * (xyY_blue[0] - xyY_green[0])
42 y_t = xyY_green[1] + t * (xyY_blue[1] - xyY_green[1])
43
44 # Convert to darktable UCS
45 xyY = np.vstack([x_t, y_t, 1]).T
46 u, v = dt_UCS_xy_to_UV(xyY)
47
48 # Get the hue angle in darktable UCS
49 angle = np.arctan2(v[0], u[0]) * 180 / np.pi
50 angle_round = np.round(angle)
51
52 if(np.abs(angle - angle_round) < 0.02):
53 index = int(angle_round + 180)
54 index += 360 if index < 0 else 0
55 index -= 360 if index > 359 else 0
56 LUT[index] = (u[0]**2 + v[0]**2)**0.5The above code runs in roughly 4s on Intel Xeon.
#Acknowledgments
This research has been financed by the community of darktable users, through my crowdfunding source.
I would like to thank Troy James Sobotka for keeping me well fed with premium academic papers and for the valuable pointers and reviews he gave me all along this work.
I also extend my gratitude to Luke Hellwig for granting me access to valuable submitted but unpublished material.
The sweeps and Munsell colours database were made from the Python library Colour Science, with some help from its main developer, Thomas Mansencal.
All of this work was made using open source libraries, computations were done in Python under Jupyter notebook, with Numpy, Scipy, Numba, Pandas, Sympy, Matplotlib and Plotly libraries.
CIE TC 1-48. Cie 1976 uniform colour spaces. In CIE 015:2004 Colorimetry, 3rd Edition, pages 24. 2004. URL: http://www.cie.co.at/publications/colorimetry-3rd-edition . ↩︎
Mark D. Fairchild. IPT colourspace. In Color Appearance Models, pages 6197–6223. Wiley, third edition, 2013. ↩︎
Muhammad Safdar, Guihua Cui, Youn Jin Kim, and Ming Ronnier Luo. Perceptually uniform color space for image signals including high dynamic range and wide gamut. Optics Express, 25(13):15131, June 2017. URL: doi:10.1364/OE.25.015131 . ↩︎
Björn Ottosson. A perceptual color space for image processing. 2020. URL: https://bottosson.github.io/posts/oklab/ . ↩︎ ↩︎ ↩︎
KIRK, Richard A. Chromaticity coordinates for graphic arts based on CIE 2006 LMS with even spacing of Munsell colours. In : Color and Imaging Conference. Society for Imaging Science and Technology, 2019. p. 215-219. URL: https://www.ingentaconnect.com/content/ist/cic/2019/00002019/00000001/art00038 . ↩︎ ↩︎
CIE S 017:2011, 17-139. URL: https://cie.co.at/eilvterm/17-22-074 ↩︎
CIE S 017:2011, 17-1136. URL: https://cie.co.at/eilvterm/17-22-073 ↩︎
CIE S 017:2011, 17-111. URL: https://cie.co.at/eilvterm/17-22-059 ↩︎
CIE S 017:2011, 17-233. URL: https://cie.co.at/eilvterm/17-22-072 ↩︎
Hue, Value, Chroma. David Briggs. Website. URL: http://www.huevaluechroma.com/093.php ↩︎
EVANS, Ralph M. et SWENHOLT, Bonnie K. Chromatic strength of colors: dominant wavelength and purity. JOSA, 1967, vol. 57, no 11, p. 1319-1324. URL: <https://doi.org/10.1364/JOSA.57.001319> ↩︎ ↩︎
VALETON, J. M. et VAN NORREN, Dirk. Light adaptation of primate cones: an analysis based on extracellular data. Vision research, 1983, vol. 23, no 12, p. 1539-1547. doi.org/10.1016/0042-6989(83)90167-0 ↩︎ ↩︎
LEDDA, Patrick, SANTOS, Luis Paulo, et CHALMERS, Alan. A local model of eye adaptation for high dynamic range images. In : Proceedings of the 3rd international conference on Computer graphics, virtual reality, visualisation and interaction in Africa. 2004. p. 151-160. URL : doi.org/10.1145/1029949.1029978 ↩︎ ↩︎
LI, Changjun, LI, Zhiqiang, WANG, Zhifeng, et al. Comprehensive color solutions: CAM16, CAT16, and CAM16‐UCS. Color Research & Application, 2017, vol. 42, no 6, p. 703-718. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
L. Hellwig and M. D. Fairchild, “Brightness, lightness, and chroma in CIECAM02 and CAM16,” Col. Res. Appl. [submitted], 2021. ↩︎ ↩︎
NEWHALL, Sidney M., NICKERSON, Dorothy, et JUDD, Deane B. Final report of the OSA subcommittee on the spacing of the Munsell colors. josa, 1943, vol. 33, no 7, p. 385-418. <https://doi.org/10.1364/JOSA.33.000385> ↩︎
MACADAM, David L. Photometric relationships between complementary colors. JOSA, 1938, vol. 28, no 4, p. 103-111. doi.org/10.1364/JOSA.28.000103 ↩︎ ↩︎
PRIDMORE, Ralph W. Model of saturation and brightness: Relations with luminance. Color Research & Application, 1990, vol. 15, no 6, p. 344-357. https://doi.org/10.1002/col.5080150609 ↩︎ ↩︎
M. A. Branch, T. F. Coleman, and Y. Li, “A Subspace, Interior, and Conjugate Gradient Method for Large-Scale Bound-Constrained Minimization Problems,” SIAM Journal on Scientific Computing, Vol. 21, Number 1, pp 1-23, 1999. ↩︎
HELLWIG, Luke, STOLITZKA, Dale, FAIRCHILD, Mark D. : Extending CIECAM02 and CAM16 for the Helmholtz-Kohlrausch Effect. [Submitted], 2021. ↩︎ ↩︎ ↩︎
WITHOUCK, Martijn, SMET, Kevin AG, RYCKAERT, Wouter R., et al. Brightness perception of unrelated self-luminous colors. JOSA A, 2013, vol. 30, no 6, p. 1248-1255. doi.org/10.1364/JOSAA.30.001248 ↩︎ ↩︎
SANDERS, C. L, and WYSZECKI, G. : Correlate for brightness in terms of CIE color matching data. Commission Internationale de l’Eclairage, Proc. 15th Session, Vienna, 1963; ↩︎
FAIRCHILD, Mark D. et PIRROTTA, Elizabeth : Predicting the lightness of chromatic object colors using CIELAB. Color Research & Application, 1991, vol. 16, no 6, p. 385-393. ↩︎ ↩︎
WYSZECKI, GÜNTER (1967) : Correlate for Lightness in Terms of CIE Chromaticity Coordinates and Luminous Reflectance. josa/57/2/josa-57-2-254.pdf, 57(2), 254–0. doi:10.1364/JOSA.57.000254 ↩︎
NEWHALL, Sidney M., NICKERSON, Dorothy, et JUDD, Deane B. Final report of the OSA subcommittee on the spacing of the Munsell colors. josa, 1943, vol. 33, no 7, p. 385-418. doi.org/10.1364/JOSA.33.000385 ↩︎
JUDD, Deane B. et WYSZECKI, Günter. Extension of the Munsell renotation system to very dark colors. JOSA, 1956, vol. 46, no 4, p. 281-284. ↩︎
JUDD, D. B. : Report of U.S. Secretariat Committee on Colorimetry and Artificial Daylight. In Proceedings of the Twelfth Session of the CIE, Stockholm (vol. 1, pp. 11), 1951. Paris : Bureau Central de la CIE. ↩︎
Sony Imaging Products & Solutions Inc. Color matching between BVM-HX310 and BVM-X300. White paper, 2020. URL: https://pro.sony/s3/2021/01/22153635/Monitor_Colormatching_v100_201222_E.pdf ↩︎
NAYATANI, Yoshinobu. Simple estimation methods for the Helmholtz—Kohlrausch effect. Color Research & Application: Endorsed by Inter‐Society Color Council, The Colour Group (Great Britain), Canadian Society for Color, Color Science Association of Japan, Dutch Society for the Study of Color, The Swedish Colour Centre Foundation, Colour Society of Australia, Centre Français de la Couleur, 1997, vol. 22, no 6, p. 385-401. ↩︎
