Filmic, darktable and the quest of the HDR tone mapping

Darktable  is an open-source software for raw photographs management and processing developped since 2009 for Linux desktops. Since then, it has been ported on Mac OS and Windows 7, 8, 10. After having used it for 7 years, I begun to develop in it 3 months ago. This article shows my work and results to improve the HDR-scenes handling in darktable, in a fashion that allows better color preservation for portrait photography.

The beginning of this article is mostly directed toward a general audience, until the section Controls, which provides a complete manual showing how to use the new filmic module. The next sections are mostly directed at scientists and technical audience.

About HDR and dynamic range

Even though HDR is a big thing right now in the LED screen industry, and this term is wildly used to describe anything for marketing purposes, it is useful to recall what it is. The dynamic range is the interval of measurement between the sensor detection level (ground level) and its saturation level (ceiling level). Any variation of the signal happening beyond this range will be recorded the same as its closest bound, which means no gradient is recorded outside the dynamic range.

While the dynamic range of the average human eye is estimated between 22 to 24 EV, consumers displays reach roughly 10 EV, 8 bits JPEG files can, because of their OETF, encode up to 12.67 EV, but paper prints have a dynamic range as low as 5 to 7 EV. This has quickely become a problem with high-end DSLR reaching now almost 15 EV (Nikon D7200, D750, D810, D850, Sony A7 , A7 RIII, Hasselblad X1D, Pentax K1, 645z).

Although “HDR” in photography has often the meaning of multi-exposure stacking and tone mapping technic (to compensate for the low dynamic range of now outdated cameras), an high dynamic range can be generally defined as any source dynamic range that is higher than the dynamic range of the destination medium. That triggers the need to remap the input dynamic range to the output one in a fashion that prevents clipping and retains as much detail as possible, for the sake of legibility. In signal processing terms, the subjective concept of “details” can be understood as local gradients in the 2D image signal, as opposed to the typical signal clipping that leads to flat surfaces where detailed content is expected.

This is a technical challenge, leading to some trade-offs, and can be done in two different (and perhaps combined) ways: ¹

1. with local tone mapping, using local contrast preservation algorithms, often resulting in halos and unrealistic pictures,
2. with global tone mapping, aiming at photographic tone reproduction, derived from Ansel Adam’s classic zone system, using global transfer functions, often resulting in color issues and local contrast compression.

Darktable has 3 modules implementing such transformations (tonemapping, global tonemapping and base curve) but their problem is they come too soon in the pixel pipe (which has a fixed order of filter application), some before the input color profile, some others working in Lab color space, introducing non-linearities in the RGB signal that often make the colour editing tedious and unpredictable : the tonemapping will shift hues and affect color saturation in unwanted ways.

About Darktable’s filmic module

The new Filmic module is a photographic tone reproduction filter aimed at reproducing the color and luminance response of analog film, dealing with dynamic range issues and gamut clipping issues (oversaturation in deep shadows and highlights). It derivates from the filmic module introduced into Blender by Troy James Sobotka, but differs in some aspects of the implementation and adds more features.

The whole idea of tonemapping/dynamic range scaling implies that trade-offs have to be made to overcome the dynamic range shrinking. The choice that has been done here is to degrade the photography in a visually-pleasing way because traditionnal film has already shaped our visual aesthetics.

For all practical purposes, filmic is a dignified tonecurve. But let us not forget that the tonecurve is the mean, and focus on the intent and on the goals.

It works in three steps:

1. apply a parametric logarithmic shaper, used to rescale the RGB values in a perceptually uniform space,
2. create an “S” filmic tone curve to bring back the contrast and remap the logarithmic grey value to the display target value,
3. do a selective desaturation on extreme luminance values, to push the colors to pure black and pure white.

By design, it will compress the dynamic range and the gamut (by reducing the saturation in bright and dark areas) in a way that preserves the mid-tones and compresses more aggressively the extreme luminances. This is especially useful when doing portrait photography, where skin tones are usually close to the middle grey, but it will need an extra care in landscape photography, especially for sunset pictures where the sun is in the frame background.

The filmic curve it produces simulates the tone response of classic film, with a linear part in the middle (called the latitude), and curved parts at the extremities (a toe and a shoulder). This kind of curve is similar to the presets applied by cameras manufacturers in their in-camera JPEG processors, and that can be found in the base curve module of darktable. However, these curves are applied too soon in darktable’s pipe and are not parametric. Filmic will essentially fulfill the same needs with some additional sweeteners and more configuration.

Place in the workflow

Most users will need to reconsider their workflow to fully take advantage of filmic.This module should be enabled after :

1. the white balance module, in order to work on balanced RGB ratios,
2. the exposure module, if needed, to recover as much dynamic range as possible in a linear way,
3. the demosaicing module, using high quality algorithms with color smoothing, to avoid artifacs in low-lights that could perturbate the auto-tuner of filmic (especially the black exposure).

Proper exposure settings can be checked prior to filmic use, using the global color picker Lab readings, and are achieved when:

2. no pixel has a luminance lower than 0 %,
3. white skins have an average lightness $L^*$ of 65-85 % in CIE Lab 76 space
4. black skins have an average lightness $L^*$ of 25-45 % in CIE Lab 76 space
5. tanned skins have an average lightness $L^*$ of 45-65 % in CIE Lab 76 space
6. non-human subjects have an average lightness $L^*$ around 50 % in CIE Lab space (excepted deliberate use of low-key or high-key)

Color corrections should come before this module. It can replace base curves, tone curves (to some extent), unbreak color profile, global tonemapping and shadows-highlights modules. It is not recommended to use it in combination with base curves, unbreak color profile and global tonemapping.

Use cases

Samples

0. The original shows the raw file with white balance fixed and sensor RGB remapped to sRGB. The file is corrected in exposure (linearly) as to remap the dynamic range into display space while preserving original chromaticity.
1. the classic darktable edit makes use of the Sony-like base curve and the tonemapping module (defaults parameters),
2. the default filmic output makes use of the filmic v1 module (2018) only with default parameters, then grey sets at 1.28 % and latitude sets at 6.50 EV (settings as shown in the above screenshot),
3. the filmic variant 1 enables the chroma preservation in filmic and decrease the extreme saturation to 20 %.,
4. the filmic variant 2 is similar to the variant 1, with saturation decreased at 75 % in the color balance module,
5. the filmic v7 variant shows the combined effect of the guided laplacians highlights reconstruction (introduced in 2021), the filmic highlights reconstruction (introduced circa 2020), and the filmic v7 color science (introduced in 2023).

After

Before

This shot was taken in July at around 2 p.m., under trees. The color recovery is quite challenging since there is direct sun light as well as green light reflected by the foliage and the grass, so the camera adjusted the white balance to revert the green cast by shifting the tint, making the direct sunlight look magenta. The white balance used here is the one set by the camera.

1. the classic darktable edit makes use of the Nikon-like alternate base curve and the tonemapping module (defaults parameters),
2. the default filmic output makes use of the filmic module only with default parameters and grey sets at 2.87 % and latitude at 6.14 EV,
3. the variant 1 enables the chroma preservation in filmic, with saturation set at 15 % in filmic and the saturation set at 65 % in the color balance module
4. the variant 2 is is the same as the previous but with the grey value adjusted to get a more natural skin tone (2.44 %), saturation at 12 %, latitude at 7 EV, and further editing in the color balance module, to remove the green color cast from the light reflected by the foliage and the grass.
5. the variant 3 derivates from the previous, increases the contrast at 1.555, reduces the latitude to 6.10 EV, the saturation to 10 %, and uses an extra RGB S curve in the tone curve module.

Note : you can download the JPEG files and import the darktable settings  directly from their embedded XMP tags as if they were XMP sidecar files.

Analyse

The sunset picture shows the advantages and the limits of the filmic module : while the local contrast is better preserved in shadows, with improved sharpness compared to the tone mapping version, the highlights get more compressed and heavily desaturated without the chroma preservation. There are several ways to overcome this issue :

• increase the saturation parameter above 100 %,
• use a parametric mask to exclude partially or totally the highlights.

The desaturation, while expected and desirable, is excessive in highlights with the default parameters. This can be compensated by adding more saturation in another module, color balance for example, or by using the chrominance preservation option in filmic (see below). In this case however, the problem is reverted and the saturation becomes excessive, so it needs to be dampened instead.

The chrominance preservation keeps more saturated colors, all over the dynamic range. Despite its goal to retain the original RGB ratios (relatively to the luminance), and therefore avoid hue shifting, the very bright areas of the sky shift nonetheless from orange to pink. The causes of this shift will be analysed in the section Discussion.

The second picture shows clearly the benefit of the filmic approach in portrait photography. The grey level is the key to get the right skin tone. The selective desaturation in highlights prevents the skin patch exposed to the direct sunlight from becoming either magenta or yellow, and the magenta highlights of the red dress shown in the classic darktable edit are avoided.

Comparison with other darktable’s tonemapping methods

Samples

The method for the local contrast and base curve is taken from Johannes Hanika². The color of the dress is vivid red (not magenta).

Analyse

Luminance mapping

In terms of tonemapping, the only good results are given by the base curve (6) using the exposure fusion, the filmic module (7, 8) and the tone curve in RGB (9).

The tone curve approach (9) is a naive transfer function roughly similar to a logarithm (see curve displayed next). Although it gives a rather good tone mapping from afar, it does not retain well the local contrast in shadows. This is the very reason why most tonemapping algorithms use spatial filters to retain the high frequencies. This method also has the drawback of being fastidious to set, from the position of nodes. It is roughly similar to the filmic without chroma preservation (8), except for the lowlights.

The base curve with exposure fusion (6) gives a result very similar to the filmic module with chroma (7), but with more contrast in shadows due to the Nikon-like alternate curve having a toe in low-lights. However, since this module is at the beginning of the pixel pipe, it turns the raw RGB space into display-referred (non-linear) space too early, making further color edits more unpredictable. To get results similar to the base curve, with filmic, one should add an extra tone curve to get more contrast. However, the main drawback of the exposure fusion, that is not shown here, is the creation of halos along sharp contrasted edges, induced by the gaussian mask used for the fusion.

The filmic approach with chroma preservation (7) gives a slightly darker result than filmic without the chroma preservation (8), due to the extra-saturation that also affects human lightness perception. With chroma preservation, the saturation adjustment can be a bit tedious to set since there is no accurate model to generally remap the saturation according to the tonemapping intensity (see section Discussion).

The global tonemapping options don’t fully recover the dynamic range and flatten a lot the local contrast, even when increasing the details preservation parameter. It comes as a surprise, because the algorithms used in there give better results in the litterature³⁴ and the filmic module approach is very similar to the Drago’s one. This may be explained by the fact that these algorithms were designed to work in linearly encoded RGB spaces or on scene-referred luminance while they are implemented in darktable in Lab space and rather late in the pixel pipe. The global tonemapping using the Reinhard method is most probably broken since it does not allow output luminance values above 66 % in Lab, even when increasing the exposure.

The shadows/highlights approach is very limited since it is a simple dodging and burning mask, feathered with gaussian or bilateral blurs. It gives a small latitude of adjustement and show halos and artefacts as soon as the parameters get higher. It creates here a parasite glare on the dress.

The method suggested by Johannes Hanika can display good results, although it’s a mixed and fastidious approach that involves tone and spatial uncorrelated corrections, since 3 different modules are involved and not controlled in a parametric way. This gives a poor repetability.

Color preservation

Out of the 6 samples proposed here, the only one where the dress color did not bend towards magenta is the filmic with chroma preservation (7), although it is slightly over-saturated. The chroma preservation variant therefore needs a manual correction on the saturation.

The global tonemapping methods (1, 2, 3) show desaturation in shadows and saturation artifacts on the contours of the sunlit skin patch.

The base curve method with exposure fusion (6) gives an overall nice saturation but shifts the hue of the dress towards magenta, especially the highlights. So does the filmic module without the chroma preservation (8). This is because both algorithms are applied separately on RGB channels.

Final results after full editings using only filmic (with chroma preservation) and color balance modules

Controls

It is important to understand that this module is roughly a combination of the unbreak color profile module in logarithmic mode and the tone curve module, with additional sweeteners, for a specialized use. The parameters offered in the user irterface (UI) are intended to build a tonecurve in an assisted way, therefore, not every parameter combination leads to a valid curve and the graph will help you diagnose problems (see the section Known issues below). Also, usually correct values are provided below as general guidelines.

The controls are displayed in the same order they should be set. The best results will be obtained when the photograph has been exposed “to the right”, meaning that the in-camera exposure has been adjusted so that the extreme highlights are on the verge of clipping. Very few cameras have an highlight-priority exposure mode, so this will be achieved, most of the time, by manually under-exposing the shots with exposure compensation.

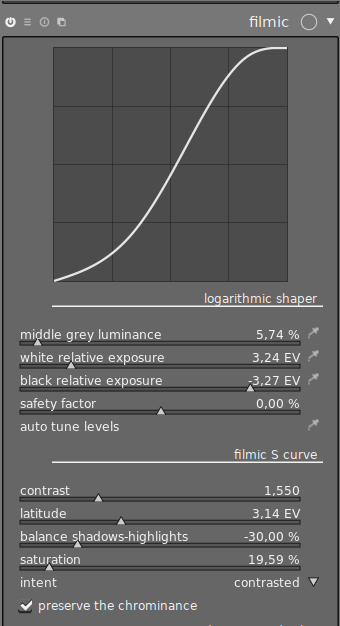
Logarithmic shaper

The logarithmic shaper raises the lightness of the mid-tones, recovers the low-lights, and remaps the whole dynamic range inside the available luminance bounds (0-100 %). It is equivalent to the unbreak color profile in logarithmic mode.

Parameters

Middle-grey luminance

The middle-grey luminance is the luminance of the scene-referred 18% grey. If you have a color-chart shot (IT8 chart or colorchecker), the color-picker tool, on the right of the grey slider, can be used to sample the luminance of the grey patch on the picture. In back-light situations, the color-picker can be used to sample the average luminance of the subject. This setting has an effect on the picture that is analogous to the lightness setting, values < 18 % will increase the lightness of mid-tones, values > 18 % will decrease it, values == 18 % will keep them as shot by the camera.

Correct values:

• Low-dynamic range pictures (6-9 EV) : 12-18 % (studio & controlled lighting, indoors, overcast weather)
• High-dynamic range pictures (9-15 EV): 2-12 % (back-lit portraits, landscapes),
• never higher than 20-22 % : that would mean the picture is globaly over-exposed and need to be fixed in exposure module beforehand,
• in general : the larger the dynamic range of the scene is, the lower the grey value should be set.

Images with a properly-set grey value often show a peak in their histogram around 50 % luminance. When the grey value is changed, the white and black exposures are automatically adjusted so the ratio white/grey and grey/black are always retained. It is advised to set coarsly the grey value, then the white and black exposures, and to finally fine-tune the grey value once again until mid-tones have a proper lightness.

White relative exposure

The white relative exposure is the upper bound of the dynamic range. It should be adjusted such that the pure white is remapped at the extreme right of the histogram. To do so automatically, you can use the color-picker on the white exposure slider and sample the whole image. The software will then record the maximum value over the area, assume it is pure white, and adjust the parameter adequately to remap it to the right bound of the histogram. This setting has an effect on the picture that is analogous to the white point setting in the levels module. When you have no pure white in the picture, for example if the maximum luminance is skin, you need to give the white some more room to avoid over-exposure of the skin, using the safety factor set around 20-33 %.

Correct values:

• 2 to 3 EV when the gray is set at 18 %,
• up to 7 EV when the grey is lower.

Value < 2 EV will usually fail to deliver proper results, except if the shot has been under-exposed, but that should be corrected in the exposure module first.

Black relative exposure

The black relative exposure is the lower bound of the dynamic range. On the contrary to the white exposure, which is determined technically by the maximum RGB value of the picture, the black exposure setting is up to you and to the amount of details you need to recover in the shadows, at the expense of the global contrast. Using the color-picker, the software will detect the minimum value of the selected area, assume it is pure black and adjust the parameter adequately. This setting has an effect on the picture that is analogous to the black point setting in the levels module.

Correct values:

• -6 to -12 EV when the grey is set at 18 %,
• up to -4 EV when the grey is lower.

Keeping the $\text{black exposure} \approx - \text{white exposure}$ makes the curve easier to control. Values > -4 EV will usually fail to deliver proper results.

General notes on the dynamic range

If you know beforehand the dynamic range of your camera at the current ISO (for example, from the website dxomark.com  or dpreview.com ), you can set the white exposure from the color-picker measurement and then adjust the black exposure from the given dynamic range :

$$\text{dynamic range} = \text{white exposure} - \text{black exposure}$$

Example: If you have a white exposure of 3.26 EV and your camera has a dynamic range of 14,01 EV. The black exposure should be set to -10.75 EV.

In natural light setups, with even distributions of luminance (landscapes), you can use the color-picker labelled “auto-tune levels” to try automatically set these 3 values at once. The auto-tuner will make some assumptions that give fair and quick results most of the time, but may need some adjustments. The auto-tuner will usually fail to deliver adequate values in controlled lighting (studio or indoors), especially if the scene is a low-key or a high-key.

The safety factor allows for shrinking or enlarging the dynamic range (that is, the black and white exposures) all at once, both in the current settings and in the automatic detection. In most cases, the dynamic range should never be lower than ~ 6 EV nor higher than the theoritical dynamic range at the used ISO measured by DXO Mark (that is maximum 14.9 EV at 60 ISO for the best high-end cameras).

Filmic S curve

The filmic S curve is a tone curve modeling the tone response of film. It is very similar to the tone curve module, the difference being filmic offers an assisted set-up from the output of the logarithmic shaper and some additional “human-readable” intent related to the behaviour of film. The curve is designed to remap the grey level to an user-specified value, relative to the output medium. Finally, it desaturates the extreme luminances to make them slide toward pure black and pure white. While this is to emulate the film color rendition, it is mostly useful to prevent gamut clipping.

The filmic curve is created by interpolation of nodes, which are positionned on the graph from the user’s parameters. The nodes are shown on the graph to give a better overview of the parameters impact on the curve, but cannot be manipulated directly. Said curve has 4 nodes by default: black, lower bound of the latitude, upper bound of the latitude, and white. The curve is adjusted so that the center of the graph (50, 50) % is always mapped to the middle grey and the S curve becomes symmetrically centered on both axes, and easier to read.

Parameters

Contrast

The contrast sets up the slope of the linear part of the S curve. It needs to be high enough to avoid inversed S branches and cusps that would invert the contrast, but low enough to avoid overshoot of the branches and cliping. The contrast will mainly affect mid-tones, which are inside the bounds of the latitude, and fill make the curve rotate around the grey node. The contrast parameter can be seen as the “tension” of the curve : the more the dynamic range is increased, the more the contrast needs to be raised to avoid inverted S branch that would flatten the contrast.

Usual values :

• dynamic range of 8–10 EV : 1.4 – 1.5
• dynamic range of 10–12 EV : 1.5 – 1.6
• dynamic range of 12–14 EV : 1.6 – 1.7

Latitude

The latitude controls the range of the linear part in the center of the curve. A low latitude will give more pronounced curly branches which will make the image look more faded at the extremities, with smooth transitions. A high latitude will give more contrast at the extremes luminances. The latitude will not change, however, the contrast in mid-tones. It has an upper bound at 95 % of the dynamic range. Also, in some setups, a high latitude removes curly branches and smooth transitions at the extremities, giving flat and linear ends that will most likely clip values. To avoid that, reduce the latitude, the contrast or both.

Usual values :

• generally : between one fourth and one half of the dynamic range,
• when grey = 18 % : around 2 EV,
• when grey = 9 % : around 3 EV,
• when grey = 4.5 % : around 4 EV
• when grey = 2.25 % : around 5 EV
• when grey = 1.13 % : around 6 EV

I advise you to try keeping the latitude as large as possible, while adjusting the contrast to stay barely avoid overshoots and clipping. The latitude also controls the center and the width of the desaturation mask : the center of the latitude is not desaturated, the insides of the latitude are barely desaturated, and the outsides get desaturated more and more toward achromatic tones.

Balance thadows/highlights

The balance shadows/highlight allows more room to one extremity of the histogram, in order to preserve more details. It is also useful to avoid flat, clipped ends in some latitude/contrast setups. It will slide the latitude along the slope without affecting the mid-tones. Generally, it is good to tune the balance so that the latitude is centered on the graph. A centered latitude can then be expanded with a minimized risk of clipping and will desaturates the extreme luminances symetrically.

Usual values: 0 ± 10 %.

Saturation

The saturation setting controls how much the extreme luminances will be desaturated to reverse the side-effects of the RGB tone curve, to avoid gamut-clipping as well as to give a more classic filmic look. This will mostly have an effect in deep shadows and harsh highlights. When set too harshly (values < 5 %), the desaturation produces a banding effect on colors in shadows : this is a sign you went too far. The actual desaturation mask uses the latitude and the saturation parameters to set-up the width of the unmasked portion, so is is advised to keep the saturation parameter at 100 % while setting the latitude, then use the saturation parameter to fine-tune it.

Usual values:

• whitout chroma preservation : 100 % is usually fine, it will provide minimal desaturation on the extreme luminances,
• with chroma preservation : 11-55 %,
• more than 100 % with cancel the desaturation but not actually add more saturation,
• 0 % turns the picture in pure black and white, based on the XYZ luminance.

To use saturation values upper than 200 % (and ensure virtually no desaturation at all), click with the right button on the slider and input any value between 200 and 1000 % from the keyboard. These is especially useful when using very low latitudes while no stiff desaturation is intended.

Chrominance preservation

When the chroma preservation is not enabled, the image will be processed in ProPhoto RGB space using the same transform on the 3 RGB channels independantly. This will generally desaturates the highlights and resaturate the lowlights, but will also produce some hue shifting (red will shift towards magenta, orange toward yellow, blue to cyan etc.). This mode is usually suitable for low-dynamic range and sometimes needs to add more saturation in another module (color balance, for instance).

The chroma preservation saves the RGB ratios before the logarithmic shaper and processes only the maximum of the 3 channels in the filmic pipe. At the output, the RGB ratios are applied back to restore the colors. This will ensure the radiometric RGB ratios are kept intact, but will most of the time produce over-saturated colours that need to be dealt with separately (in color balance, good output saturation values are usually 75 to 85 % to correct the oversaturation). This mode is usually more suitable for high-dynamic range pictures, to avoid color shifting, are when precise color corrections are performed (color-grading) and need to be retained untouched, but needs an extra step to correct the saturation manually. Also, keep in mind that preserving the color ratios while changing their luminance does not affect colors in a perceptual way.

An efficient workflow would be to start setting the module with chroma preservation disabled, then, as a last step, enable it to see if it brings an additional benefit to your picture. After the chroma preservation is enabled, adjust the output desaturation in color-balance to approximately 80 % to get the mid-tones properly saturated. As a last step, fine-tune the saturation parameter of filmic to have the extreme tones properly desaturated.

Notice that the chroma preservation is especially not forgiving with inaccurate color profiles and color-checker LUTs, ill-set white balances, and lens chromatic aberrations. The white balance settings will often need an extra fine-tuning after having set filmic.

Intent

The intent choice controls the interpolation method of the curve. The “contrasted” intent uses a cubic spline interpolation that produces gracious rounded curves leading to more contrast at the extreme luminances. However, it is quite sensible to the node position and often degenerates when they are too close, producing cusps and flat clipped ends. The “linear” intent uses a strictly monotonic Hermite spline interpolation. The branches of the “S” are less gracious, more linear, resulting in less contrast at the extremities, but this spline is more robust and easier to control. The “faded” intent uses a Catmull-Rom centripetal spline that is guaranteed to avoid cusps, strange behaviours, and is the most robust. However, it doesn’t look as good and give a sort of “retro” faded look. The “optimized” intent is an average between the linear and contrasted intents that produces a good trade-off most of the time.

Destination/Display

These are the parameters of the screen or the output color profile for which we need to remap the white, grey and black levels at the output of the logarithmic shaper. 99 % of the cases, these parameters should remain untouched.

The middle grey value should never be touched if your output/display profile is a standard RGB profile where the grey is defined as 18 %.

The output power factor is the gamma of your screen or the gamma set in your ICC output profile. Unless you use ProphotoRGB (gamma = 1.8) or linear spaces (gamma = 1.0), you should not change that parameter.

The output grey target to remap the logarithmic grey point is computed as follow: $\text{output grey}^{\frac{1}{\text{gamma}}}$.

The white and black luminance should always stay as is, unless you want a “retro” faded look with raised blacks and dampened whites.

Known issues

In noisy pictures, or in pictures that suffer from poor demosaicing (RAW from X-trans sensors), the black level will often be detected at -16 EV (minimum of the range). You need to correct that manually to obtain realistic values.

When the dynamic range is really off-center (e.g. white at +2 EV and black at -13 EV), the filmic S curve can have a really hard time building a proper S curve. To do so, you can either decrease the grey level to increase the white exposure (which can work well in landscape photography, but might make skin tones too bright) or use the black level from the exposure module to slide the RGB values to the right (negative values in the black slider).

When the dynamic range is not more or less zero-centered, and the black exposure is very far from the white, the curve doesn’t look like an “S” but might hit the ground or the ceiling of the graph closer to the middle than expected.

In some setups, some settings (mostly contrast and latitude) will have fulcrum values where the aspect of the curves differs strongly between two very close setting values. This is because some settings put nodes in bad places (< 0, for example), so the faulty nodes are removed and then the interpolations of the curves change.

Further editings

Any global tonemapping has its limits. To overcome the most difficult cases, it is advised to use the exposure module with parametric masks, in order to selectively push or pull the exposure in bright and dark areas (the same way as a dodge & burn), and feather the masks contours with the new guided-filter feature. This will essentially achieve the same goal as the shadows/highlights module with more latitude available, in camera RGB, and with a better feathering that the gaussian or bilateral blurs used in shadows/highlights.

The color balance module is a powerful tool to either revert parasite casts from composite lightings, or create a cinematic mood using colors. It can be used to perform subtle split-tonings and overcome the under/over-saturation induced by the filmic module.

Algorithm

The whole algorithm takes RGB code values as input, preferably in the display RGB space with scene-linear scaling (hence no EOTF or gamma).

Logarithmic shaper

The logarithmic transfer function is directly taken from the ACES as follow:

$$ y = \dfrac{\log_2 \left(\frac{x}{\text{grey}}\right) - \text{black}_{EV}}{\text{white}_{EV} - \text{black}_{EV}} $$

where $y$ is either the decorrelated RGB channels (computed one by one), or an RGB norm representing the luminance of the pixel, such as $\text{max}(RGB)$ in the chrominance preservation mode. In this mode, the RGB ratios are saved at the input, before the logarithmic function, such that:

$$ \begin{cases}R_r &= \frac{R}{\text{norm}} \\ G_r &= \frac{G}{\text{norm}}\\ B_r &= \frac{B}{\text{norm}} \end{cases} $$

The gray level acts as a pre-amplification: RGB values below input gray will be lifted far more by the logarithmic shaper than the RGB values above. Then, the black and white exposures act as normalization parameters, such that the white is remapped to 1 and the black to 0.

The value $\text{DR} = \text{white}_{EV} - \text{black}_{EV}$, at the denominator of the fraction, defines the dynamic range of the image. The user input for the S-shaped curve is :

• latitude, which is the linear part in the middle of the curve, expressed in EV, noted $\text{L}$ such that $\text{L} < \text{DR}$
• contrast, which is the slope of this linear part, noted $\text{C}$
• shadows/highlights balance, which translates the linear part to the right or to the left by following the slope, noted $\text{B}$, expressed as a ratio $\in [0 ; 1[$.

After the above logarithmic transfer function, we get the input grey remapped to $\text{G}_{log} = \frac{- \text{black}_{EV}}{ \text{DR} }$. Notice that, for classic LDR pictures (8 EV) where the middle grey is at 18 % and the white point is 2.45 EV higher (100 %), the $\text{G}_{log}$ is expected at 69 %, which is higher than its CIE Lab value.

This $\text{G}_{log}$ will then be remapped, through the S-shaped curve, to the $\text{G}_{display}$ such that $\text{G}_{display} = 0.18^{1/\gamma}$. In the current implementation, the default value of the middle grey (18 %) as well as the display gamma (2.2 by default) are user-editable, and the gamma can be set to 1 in order to get a “linear” pipeline after filmic.

Filmic tone curve

The software then translates the parameters into 2D nodes that will be fed to the interpolation algorithm:

• grey $ = \{\text{G}_{l} ; \text{G}_{d} \} \\ = \left\{ \frac{- \text{black}_{EV}}{ \text{DR}} ; 0.18^{1/\gamma} \right\}$
• black $ = \{ 0 ; 0 \}$
• white $= \{ 1 ; 1 \}$
• latitude, bottom $= \{ \text{T}_{l} ; \text{T}_{d} \} \\ =  \left\{ \text{G}_{l} × \left(1  - \frac{\text{latitude}}{ \text{DR}} \right) ; \text{C} × \left(\text{T}_{l} - \text{G}_{l}\right) + \text{G}_{d} \right\}$
• latitude, top $= \{ \text{S}_{l} ; \text{S}_{d} \} \\ = \left\{ \text{G}_{l} + \frac{\text{L}}{\text{DR}} × (1 - \text{G}_{l}) ; \text{C} × (\text{S}_{l} - \text{G}_{l}) + \text{G}_{d} \right\}$

To apply the translation from the shadows/highlights balance, we then correct the $\{x ; y \}$ coordinates of the latitude nodes by applying the following offsets:

$$ \left \{ \frac{- \text{B} × (\text{DR} - \text{L})}{\text{DR} × \sqrt{\text{C}^2 + 1}} ;  \frac{- \text{B} × \text{C} × (\text{DR} - \text{L})}{\text{DR} × \sqrt{\text{C}^2 + 1}} \right \} $$

The nodes are then fed to an interpolation algorithm (Hermite monotic splines, cubic splines, etc.) that derivates a smooth transfer function $S(y)$. For more robusts results, to avoid cusps and ensure the linearity of the latitude portion, the grey node can be ignored in the interpolation, and used only to compute the 4 other nodes that will be actually used to derivate the S-shaped transfer function.

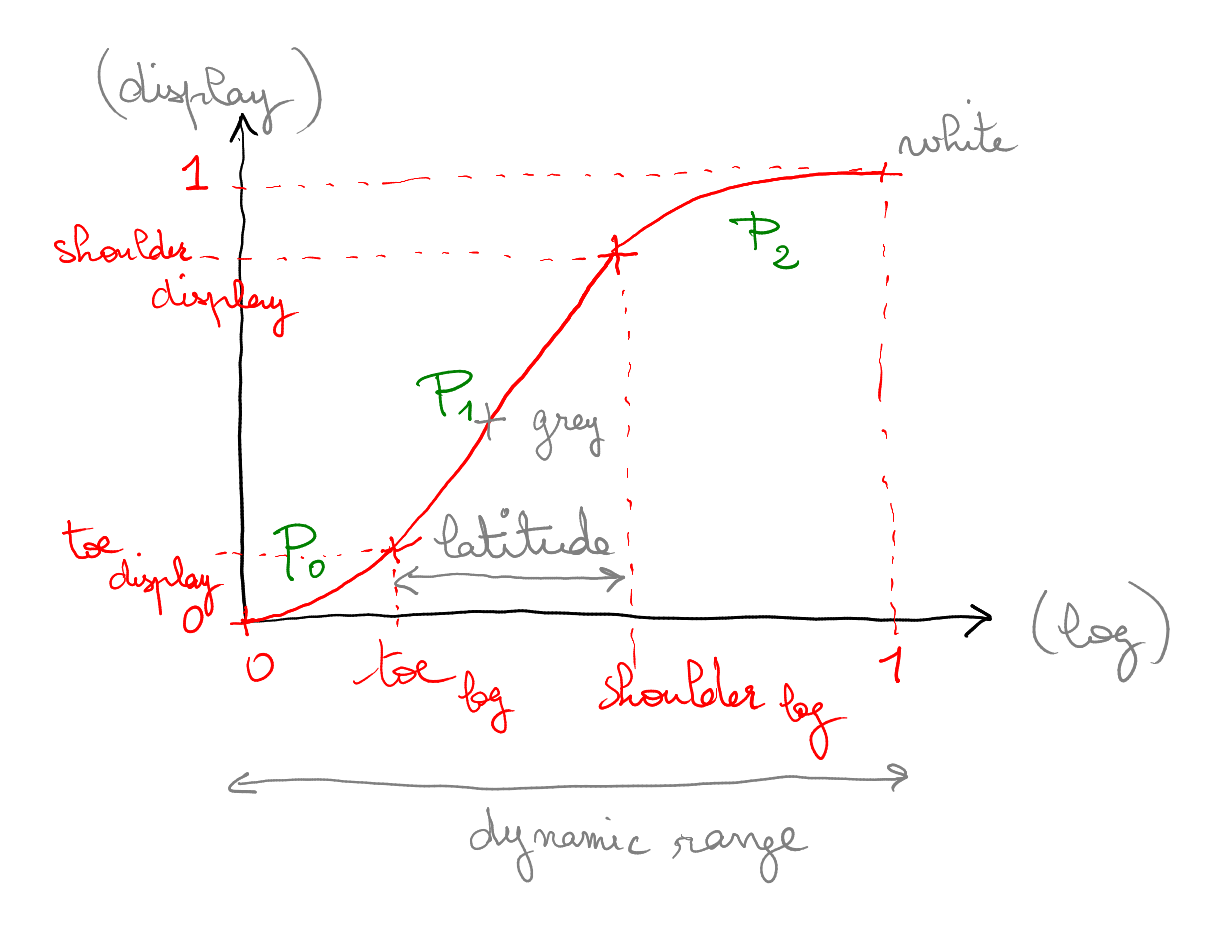
In a future version, we propose to derivate directly from the constraints and boundary conditions an interpolation by parts, where $P_0$ and $P_2$ will be polynoms and  $P_1$ would be a linear function. We wish to impose a first order and a second order continuity at the bounds of the latitude, to ensure slope and curvature continuity between the parts of the function, and a zero tangente at the extreme bounds (white and black) to avoid undershoot and overshoot. That is :

$$\begin{cases} P_1'(x) &= \text{C} \\\ P_1(\text{T}_{l}) &= \text{T}_{d} \\\ P_0(0) &= 0 \\\ P_0'(0) &= 0 \\\ P_0(\text{T}_{l}) &= \text{T}_{d} \\\ P_0'(\text{T}_{l}) &= P_1'(\text{T}_{l}) \\\ P_0''(\text{T}_{l}) &= P_1''(\text{T}_{l}) \\\ P_2(1) &= 1 \\\ P_2'(1) &= 0 \\\ P_2(\text{S}_{l}) &= \text{S}_{d} \\\ P_2'(\text{S}_{l}) &= P_1'(\text{S}_{l}) \\\ P_2''(\text{S}_{l}) &= P_1''(\text{S}_{l}) \end{cases}$$

Each polynom needs to satisfy 5 conditions, therefore we need 4th order polynoms. Let us parametrize such functions $\forall \{x, a, b, c, d, e, f, g, h, i, j, k, l\} \in \mathbb{R}^{13}$ :

$$ \begin{align} & \begin{cases} P_0(x) &= a x^4 + b x^3 + c x^2 + d x + e\\ P_1(x) &= f x + g\\ P_2(x) &= h x^4 + i x^3 + j x^2 + k x + l\\ \end{cases} \\\ \Rightarrow & \begin{cases} P_0’(x) &= 4 a x^3 + 3 b x^2 + 2 c x + d \\ P_1’(x) &= f \\ P_2’(x) &= 4 h x^3 + 3 i x^2 + 2 j x + k  \\ \end{cases} \\\ \Rightarrow & \begin{cases} P_0’’(x) &= 12 a x^2 + 6 b x + 2 c \\ P_1’’(x) &= 0 \\ P_2’’(x) &= 12 h x^4 + 6 i x + 2 j \\ \end{cases} \end{align} $$

This can be split into 3 linear sub-systems for faster resolution, the last two being solvable in parallel :

$$ P_1 : \begin{bmatrix} 1 & 0 \\ \text{T}_l & 1\\ \end{bmatrix} \cdot \begin{bmatrix}f \\ g \end{bmatrix} = \begin{bmatrix} \text{C}\\ \text{T}_d\\ \end{bmatrix} $$

$$P_0 : \begin{bmatrix} 0 & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 1 & 0\\ \text{T}_l^4 & \text{T}_l^3 & \text{T}_l^2 & \text{T}_l & 1\\ 4 \text{T}_l^3 & 3 \text{T}_l^2 & 2 \text{T}_l & 1  & 0\\ 12 \text{T}_l^2 & 6 \text{T}_l & 2  & 0 & 0\\ \end{bmatrix} \cdot \begin{bmatrix}a\\b\\c\\d\\e\\ \end{bmatrix} = \begin{bmatrix} 0\\ 0\\ \text{T}_d\\ f\\ 0\\ \end{bmatrix}$$

$$P_2 : \begin{bmatrix}  1 & 1 & 1 & 1 & 1\\ 4 & 3 & 2 & 1 & 0 \\ \text{S}_l^4 & \text{S}_l^4 & \text{S}_l^2 & \text{S}_l & 1 \\ 4 \text{S}_l^3 & 3 \text{S}_l^2 & 2 \text{S}_l & 1 & 0\\ 12 \text{S}_l^2 & 6 \text{S}_l & 2 & 0 & 0\\ \end{bmatrix} \cdot \begin{bmatrix}h\\i\\j\\k\\l\end{bmatrix} = \begin{bmatrix} 1\\ 0\\ \text{S}_d\\ f\\ 0\end{bmatrix}$$

Solving the polynomial coefficients for the input nodes can be achieved through a gaussian elimination, then, in a vectorized SIMD/SSE setup of 4 single precision floats using Fused Multiply-Add, a fast evaluation of $S(y)$ should be possible such that:

$$ S(y) = \left[ \begin{bmatrix} e \\ g \\ l\\ 0\\ \end{bmatrix} +  y \cdot \left( \begin{bmatrix} d \\ f \\ k\\ 0\\ \end{bmatrix} + y \cdot \left(\begin{bmatrix} c \\ 0 \\ j\\ 0\\ \end{bmatrix} + y \cdot \left(\begin{bmatrix} b \\ 0 \\ i \\ 0\\ \end{bmatrix} + y \cdot  \begin{bmatrix} a \\ 0 \\ h \\ 0\\ \end{bmatrix}\right)\right)\right) \right] \cdot \begin{bmatrix} (y < \text{T}_l)\\ (\text{T}_l \leq y \leq \text{S}_l)\\ (y > \text{S}_l)\\ 0\\ \end{bmatrix}^T $$ the last matrix being an boolean mask where lines are set to 1 where the condition is met, or 0 otherwise.

The above graph shows how a such interpolation could produce more contrast than the Hermite monotonic spline, with a true linear part in the middle. The proposed method, however, is more unstable and the out-of-bounds values (which should not happen if the ACES log normalization was properly set) are completely unpredictable, due to the oscillations introduced by the 4th order.

If the chrominance preservation mode is enabled, the RGB ratios are reapplied after the S-shaped transfer function, in order to recover the full tristimulus, such as:

$$ \begin{bmatrix} R \\ G \\ B \end{bmatrix} = S(y) \cdot \begin{bmatrix} R_r \\ G_r \\ B_r \end{bmatrix} $$

Selective desaturation

Then, a gaussian luminance mask, centered on the latitude, is built such that its weights are:

$$w(l) = \exp\left( \dfrac{-\left( \frac{\text{shoulder}_{display} - \text{toe}_{display}}{2} - l\right)^2}{2 \sigma}\right)$$

with $l$ the luminance, and $\sigma$ a user input. $l$ is taken after the $S(y)$ transform, and is either the $Y$ channel of the $S\left(\begin{bmatrix} R \\ G \\ B \end{bmatrix}\right)$ output converted into the $XYZ$ space if the chrominance preservation mode is disabled, or the $S(\text{norm}(RGB))$ otherwise. These weights are used to desaturate selectively the highlights and lowlights, such as:

$$\begin{bmatrix} R \\ G \\ B \end{bmatrix}_{out} = \begin{bmatrix} Y \\ Y \\ Y \end{bmatrix} + w(l) \cdot \begin{bmatrix} R - Y \\ G - Y \\ B - Y \end{bmatrix} $$

Pipeline integration

At the end of this process, the RGB signal is remapped to the display-referred space, with the middle grey raised at around 46 % ($0.18^{(1/2.2)}$), and should be sent directly to the screen. However, since darktable’s pipeline re-applies the display gamma encoding (EOTF, to be rigorous) at the end, the final step consists in reverting this gamma encoding with an $f(x) = x^\gamma$ function, to remap 46 % to 18 % grey. However, the current implementation of the chroma preservation in darktable has some trouble with this step, as pointed out by Andrea Ferrero . Figuring out a proper way to manage both is still ongoing work for filmic v3 and darktable v2.8.

Discussion

One major problem of tonemapping is the conservation of colors through the operation. The sub-problem remains yet to decide wether it is the photographic colors that should be preserved (as recorded or percieved on the scene), or the perceptual colors (as displayed on the output medium), which depends on the perceived luminance and various other parameters, depending on the color model used.

Mantiuk and al.⁵ conducted a study on saturation correction in tonemapping algorithms where they tried to use several color models (CIE LAB, CIE CAM02 and CIE LUV) to predict the color deviation happening during tonemapping. They found that none of these so-called “perceptual” non-linear color models were able to provide accurate prediction of color shifts, and that the actual perceptual color shifts were themselves non-linear when measured in these color spaces. They also tried to perform the tonemapping in CIE LAB space and got an oscillatory saturation shift. If that is so, it would mean that perceptual color models are flawed from their very premisses.

Let us recall that ad-hoc empirical models are to be fitted against some datasets, in a descriptive manner, and then evaluated by their ability to provide accurate predictions against different datasets. From Mantiuk’s results, the quality of these models is subject to caution. However, Mantiuk conducted his study on a sample of 4 to 8 people aged from 23 to 38, so my guess is he recruted his students and fellow faculty members in the break room, which would be neither a significative nor an unbiased sample. However, Mantiuk has pointed out that the goal of the tonemapping algorithms he reviewed was to retain the photographic colors, in which the perceptual metrics provided in non-linear spaces are unefficient and inadequate.

Besides the scientific arguments, the Reihnardt’s and Dragos’s tone mapping algorithms have become the poster cases of what the photo industry calls “HDR looks” (with a smirk) and have never gained traction in the movie industry, where professionals tend to be more educated than in the self-employed photographic business. Simple RGB shapers, using tone curves adapted for HDR compression, are still the go-to method, though they can exaggerate the highlights bleaching that people associate with “filmic look”.

Acknowledgements

I would like to thank Troy James Sobotka, who has been a great help and took a lot of his time to answer my questions during the development of this module. I thank Johannes Hanika, one-guy coding army who still takes time to answer every question after having developped darktable for 10 years,  Andreas Schneider/Cryptomilk and Mika/Paperdigits who proof-read the draft that led to this article, Nicolas Tissot and Andreas Schneider again for some of the raw pictures shown here, Minh-Ly who is kind enough to suffer me and has been providing her skin tones to test my algorithms for more than 2 years, the darktable.fr  community, Andy Costanza and Luc Viatour, who have supported me during this project, Rawfiner, who has been a great help to get me started with the C language, Pascal Obry, who reviewed and merged my code week after week, Mathieu Moy, who spotted tricky bugs and mistakes, and finally Jean-Paul Gauche and Philippe Weyland, who are always the annoying and necessarly first ones to test and report things that don’t work, and whose suggestions have led to substantial improvements.

License

Permission is hereby granted to copy and translate the content, including text, calculations and pictures, of this article for educational purposes.