A few weeks ago, I discovered the tiny world of tiny houses and camping-vans and found that quite amazing. However, the current commercial camping vans look pretty sub-optimal to me, because they are equipped with kitchen-style furniture, meaning heavy, stand-alone stuff made of chipwood/OSB panels 1.5 cm thick. See for yourself :


I spent 3 years working at Polytechnique Montreal on a 280 kg solar car made of carbon fiber, fiberglass and epoxy, and embedding 6 m² of solar panels on the top shell, so, seeing such a daddy’s design add around 750 kg of equipement on top of a 6 m² cargo van blew my mind in a bad way. Is it 2018 or what ? That overweight is going to be carried by a motor running with dirty fuel, and you might want to keep it minimal.
This sort of design can be the result of 2 things :
- skillfull people who know things I ignore and made cleverer choices than I could have made myself,
- dads who have been working like that for decades and see no interest into doing it better since people are still willing to buy it and the competition is pretty lame.
- the panels used for the furniture look oversize and overweight for their supposed design load. In fact I would never use agglomerated wood in a moving vehicule, the ratio resistance/weight is way too poor.
- the furniture is stand-alone (holds on its own feet like house furniture) instead of taking advantage of the van walls to take some of the load and minimize the panels size (because this furniture won't be moved, so we could use the walls to take some of the load).
In the same time, I just got a free student license for Autodesk Inventor, and as someone trained with Dassault Systems Catia v5, I’m just becoming a big Autodesk fanboy, especially its embedded Nastran mesher/shape generator that can analyse stress in the parts as we draw them and optimize their geometry to reduce the weight while keeping the performance.
So why not try and see how much I can reduce the weight ?
Materials
The first thing I did was to consider a manufacturing process and materials. For that, I would use fiberglass and epoxy because it's light, offers good performance for the price, and I can do it myself. I have some experience in composites building, so I would do the flat panels using a vacuum infusion on a glass or aluminium panel for many reasons :- it gives none to a few wet spots,
- it avoids air bubbles and ensure consistent mechanical properties (especially for tears propagation),
- it allows to control the fiber/resin ratio rather accurately,
- it gives a pretty finish without sanding (I have sanded the solar car shells for too much time after a not-so-great infusion, fiberglass is almost as hard as the sanding paper, so… been there, done that, not funny),
- it's easy to repair with new fiberglass patches (it's a common repair on boats).
Then, an “easy” way to stitch the panels together is a wet layup, which most use to do the regular parts as well, but this process is not reliable for consistent predictible mechanical performance.
#Naive Model
With that in mind, I began designing a shelving of 6 cells, with shelves made of 60×60 cm resin panels. As Inventor does not offers composites analyses, I picked plain epoxy resin as a first approach, all panels being 5 mm thick. I drew a very simple design, assuming the ceiling and the back panels of the shelf were the ceiling and the wall of the van, built as a monocoque structure. The doors that would be installed on the face are not drawn :

This weights 56.5 kg. Then, I simulated it using 400 N of load on each shelf, assuming perfect welding between the side panels and the shelves :

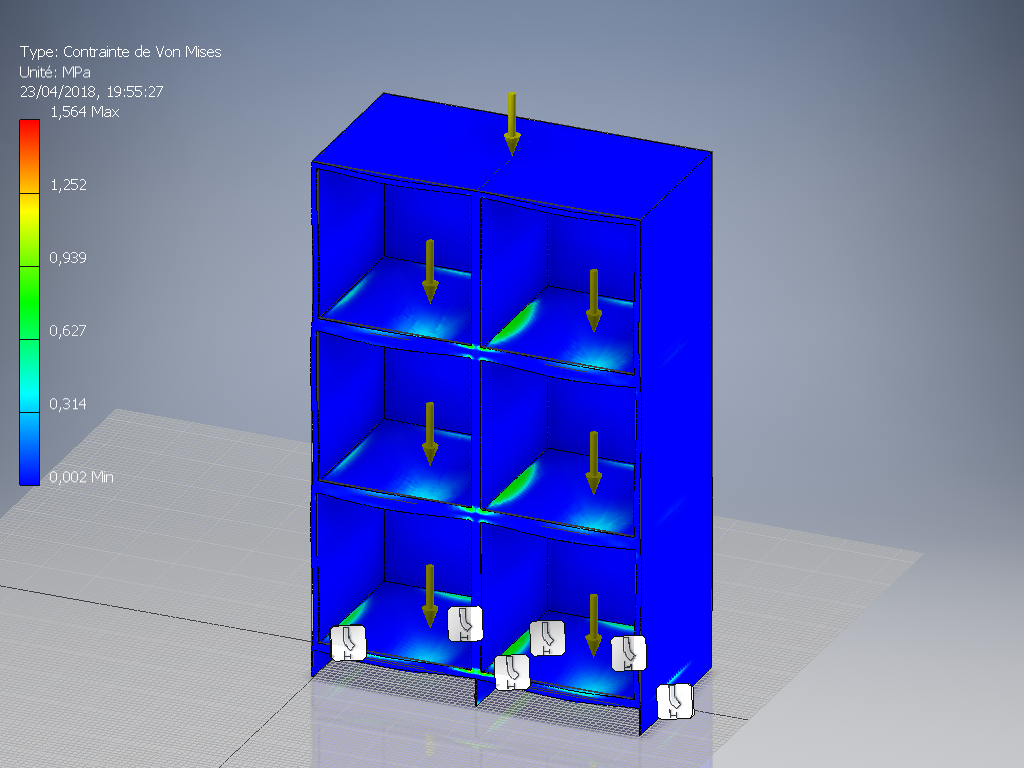

This yields a security factor of 15, a maximum deformation of 1.5 mm, and a Von Mises stress of 1.5 MPa. The security factors means that the load that can actually be supported before the material leaves its elastic domain (non-reversible deformation) is 6000 N.
Here are the material properties :
| Name | Thermoplastic resin (epoxy-like) | |
| Properties | Density | 1.28 g/cm³ |
| Yield strength | 57.2 MPa | |
| Tensile strength | 114 MPa | |
| Stress | Young modulus | 3.3 GPa |
| Poisson coefficient | 0.36 nd | |
| Shear modulus | 1.21324 GPa | |
The convergence seemed ok, but I wouldn’t trust these results with my life before I check how Inventor solver actually works and especially fails, and what it assumes. And since it’s closed source, there is no way to check it, so it’s pretty much “trust it or leave it”. An engineer is accountable for his design, and Autodesk declines all responsibility in the solver results, so it looks like one would have to export the 3 model as a STEP file and run another analysis in an opensource FEM solver. Ultimately, real-life destructive tests are the only way to validate the design.
But, let assume this is accurate and move on to the next part…
#Topologic optimization
Inventor has a very cool feature named shape generation. From what I understood, it computes the stress within the material by FEA, then remove material where the stress is close to zero, then computes the stress again with that new geometry, then iterates until the target amount of mass has been removed. It draws the output as the remaining mesh, and it is up to the designer to interprate this new contour by sketching the surfaces to remove. So it’s not entirely automatic. Besides, the software doesn’t know the manufacturing process, so it doesn’t know what shapes are actually possible to build.

This is actually a cool design, so let’s see an artistic view of it:

Of course, a van shelf would be entirely closed, but once the structure is validated, it is no big deal to glue thin non-structural sheets of composites on the sides. Additionaly, I reduced panels thickness to 3 mm. Now the whole thing weights 24.3 kg, half the initial design. Now, see what changes :



The security factor didn’t change (still 15), although the maximum deformation is now 7 mm and the Von Mises stress doubled. We are still safe. In addition, I checked this video, so I’m a bit more confident into my results and their convergence.
#Parametric optimization
Now that we have a clever geometry, it’s time to see to what extend we can reduce the mass while keeping our performance. Under a load of 400 N (roughly 40 kg), we still have a security factor of 15, with a minimum of 12.5 (obtained with further analysis) which lets a lot of room to improvement.
But let’s stop a second here. We are in a moving van, meaning everything should be safe and secured, thus enclosed. An additional static simulation shows that reducing again the thickness of our side panels to 2 mm still leads to a security factor of 9. At this point, it means that the additional closing sheets to stick to the side structure would be about the same thickness as the structural parts. But the side structure would be infused as plain panels, then cut to follow that fancy geometry, just to stick another panel on top to close it. Cutting fiberglass is not fun (been there, done that) and fiberglass dust is itchy as hell. So we decide to stuck to plain side panels and try optimizing their thickness instead of their geometry.
Now, the side panels are 1.5 mm thick, and the shelves, back panel and ceiling are 2 mm thick, for a total weight of 20.3 kg. That leaves us with a minimum security factor of 7 and a maximum deformation of 27 mm in the center of the shelves. Note that the panels are so thin that we have to use the thin body approximation for numeric stability, hence the rounded stitches are assumed to be square and the model shows stress concentrations that wouldn’t be that bad in real life (maybe).


Then, we assumed previously that the load was static, but as the van is moving, it would be periodic. The problem with dynamic loads is vibrations, defined by their magnitude and their frequency, that can trigger resonance in elastic parts. The limit of Inventor solver is it assumes the load is always external, but in dynamic regime, the force is transmitted from the wheels to the loads by the dampers and the shelves, so the loads are not external to our study anymore and we need to solve a more complex modal problem.
That’s not possible without knowing the behaviour of the van dampers, so we will have to isolate the loads in the shelves by assuming some things. Anyway, we are here merely designers so we just want to ensure our system resists to the worse possible (discrete) case of use, we don’t need to model it accurately in continuous mode.
First, we have to find the maximum frequency of the van, which is tricky because it depends on the cracks profile of the road, the speed of the vehicule, the inertia of the vehicule, and the damping coefficient from the tires and dampers. Given that a loaded van weights around 3 tons, will probably drive at 50 km/h on difficult grounds, where the maximum cracks depth would be 5 cm, and where cracks would be separated by 5 cm, we can solve the differential equation :
$$ m\ddot y = m g \times 0.05 \frac{d^2}{dt^2}\left(\cos( \frac{50000}{0.05 \times 3600} t)\right) \Rightarrow \ddot y = -393 \cos(278 t)$$
where y is the vertical displacement assuming no damping on the van.
Assuming the 40 kg loads in the shelves are strictly bonded to the van through the shelves (no jumping on the shelves), we get a maximum frequency of 44 Hz. As for the dynamic load, let’s assume a vertical acceleration of 1 G, which leads to a reaction force of 800 N from the shelves to each load. This time, we assume that the back and ceiling panels are fixed to the van trough the inside monocoque structure. Another wrong hypothesis in general use is that the alternative load is symetric, which is not because if {van + shelves} suffer more than 1 G of downward acceleration, the contact between the shelves and the loads will be lost (jumps) until impact after the acceleration reaches 0 G. But, again, we are here to ensure the worst scenario is not destructive, even if this scenario is overkill.
The results show 8 eigenmodes between 6.5 Hz and 10.5 Hz. Basically, the dynamic behaviour of the sides is like an elastic drum surface :

In the process, I discovered that this is just an analysis of the natural frequencies of the solid, not the dynamic response to a periodic perturbation. So, here, the loads count as dead intertias, not as periodic excitators, which is not what I expected. Thus, the magnitude of the deformation doesn’t count, it just shows the form of the deformation. But still, we get the problematic frequencies. The whole dynamic behavior should be modeled in more barebone FEA softwares (Comsol, Code Aster, Fenics, etc.).
To move the resonance further in higher frequencies (which are less likely to happen since our damped van is a low-pass filter), we add simple 300×5×5 mm ribs stiffeners on the sides to increase the eigenvalues. It’s the same kind of ribs you find inside guitars, on the back panel. They will be good to prevent rattle too.

The simulation becomes more computing-intensive because the approximation of the thin body is not possible anymore. So, instead of running it for hours, we can just think of a real van :
- a real van has dampers, which means the periodic load is damped after a few seconds, so, even at the critical frequencies, the system should not have enough time to reach the resonance,
- the empiric eigenmodes of a loaded van are around 0.5 - 2 Hz, which is a third of the first eigenmode of the shelf, so these destructive frequencies should rarely be reached, and if they are, they should be damped soon enough,
- more than 1 G of acceleration is probably exagerated and means passengers would need their seatbelts to avoid hurting the ceiling, which happens only in an accident.
Speaking of which, let’s check if the sides are secure enough to retain the loads in an accident where a 5 G deceleration is applied :

This is just a rough approximation, because the mechanics of impacts are more complex, and anyway, we would use fiberglass reinforcements that are not in the model right now, but we still get a minimum security factor of 1.3 in the stiching areas where the model is square but the reality will be rounded. I don’t know what the road safety regulations ask though. So just to be sure, let’s keep the side panels 2 mm thick (22 kg for the whole shelving).
#What about wood ?
Just for fun, I took the same design but replaced the 5 mm epoxy panels from the naive simulation with 1.5 cm mapple wood panels to simulate the commercial vans shelvings (Inventor does not have OSB in its database, and anyway the properties of OSB depend on its density, so… another hypothesis). The results give the same security factor of 15 but for a weight of 70 kg. This shows 2 things :
- wood is not a good material to use in weight-critical applications (nothing new here),
- the design load of each shelf of a commercial campig van might be actually around 600 N static (60 kg), which seems unlikely to happen since most shelves have 30-40 cm of height clearance. Even with a vertical acceleration of 1 G, it's still a 30 kg load, so more than an airline check-in suitcase in a third of its volume.
Keep in mind that natural mapple has about the same density than chipwood panels, between 600 and 750 kg/m³ (same as the paper). But, obviously, the actual density of the commercial shelvings is another guess.
#About safety factors
In aircrafts, due to pressing mass-reduction constraints (that is, energy efficiency constraints), security factors are set at 1.2 - 1.8. This comes with a responsibility : ensure that every load applied on the parts is well known, predictible, carefully studied and tested. There is a reason why aircrafts have a design cycle of 20 years…
Here, we are naughty kids designing stuff from a computer, using static analyses to design dynamic parts, black-boxes solvers, turning round a lot of corners, so a good practice would be to set a relatively high security factor, between 6 and 7 (as a comparison, european standards fix the safety factor for winches at 6, and 10 for elevators).
We took a reference load of 40 kg/shelf, which got us a static safety factor above 7 and a dynamic one above 1. As a comparison, 40 kg it is the mass of 24 glass bottles of 1 L each. For heavier loads, to maintain a good security factor and as we see that the stress hotspots are on the horizontal panels, we can add more shelves with less height clearance to split the loads. It is a good thing, then, to know exactly at the design stage what the purpose of the shelves will be in order to optimize their form factor and resistance. But of course, this becomes a bit overwhelming.
#Conclusion on the design
First of all, OSB/chipwood is really bad. It holds all the drawbacks of wood (poor mechanical performance for weight) and all the drawbacks of plastics (volatile emissions of carboned compounds coming from the glue and the plating).
Then, people get this wrong idea that deformation leads to destruction, so they rate the sturdyness of things using their feeling of deformation. Just see how people freak out in an airplane when the wings begin to shake back and forth. It is true that big deformations lead to destruction, but for most materials, 20 to 30 % of deformation is harmless and fully reversible. Accordingly, grand-dads over-design furniture just to comply with this wrong feeling of sturdyness.
However, the main reason for overdesigning the chipwood parts is they are assembled with screws, and you can’t screw 2 thin chipwood panels together without make one panel explode. Using fiberglass stitched “seamlessly” with wet layup, you don’t have to care about the screws clearance. So the problem comes from the material choice in the first place.
Here, using the same material (epoxy) but with a naive then computer-aided optimization, we were able te reduce the weight of the furniture by 60 %. But coming from plain woods panels 1.5 cm thick, it was 68% of weight reduction (keep in mind that the material used is probably chipwood denser and thicker). This is allowed by the monocoque embedded design and the continuous stitching of panels which gives 60×60×60 cm stiff cubic cells. Of course, this wouldn’t be possible with an height-adjustable shelf where the horizontal panels are movable and simply supported by a couple of screws.
Not only did we reduce the weight, but we maximized the available storage space, adding 0.036 m² per shelf, so 0.21 m² in total. That’s not huge, but in an 6 m² van, every bit of space is worth it.
The next step is to redo the computation using composites models, and adding delamination analysis, as well as non-linear simulations, provided by Autodesk Nastran in CAD. Then, we will get a full picture of the true potential of composites.
#Conculsion on the ROI
Of course, this optimization doesn’t come cheap. The calculation is made with two pieces of software which regular licenses are worth 2500 €/year each. Seeing the video above, where the van is built, it seems that Inventor is already used as a 3 D modeler/drawing software (or maybe it’s SolidWorks).
Then, fiberglass composites are not as straightforward as chipwood panels to work with : you need to enfuse the flat panels, let them cure, cut them, stitch them, let the stitches cure again, sand the stitches, paint and finish. The vacuum infusion uses consumables such as vacuum bags, peel ply, green flow and tubing that are all single-use. More manufacturing steps, more delays, more consumable to trash… it’s hard to compute an additional cost here without knowing the base one.
Then, of course, the base materials are more expensive than wood panels made of saw dust garbage. 18 mm chipwood with melamine plating cost 0.09 €/m², whereas mat fiberglass alone is 1.80 €/m² (for panels roughly 1 mm thick) and epoxy is 21 €/m² (assuming a resin absorption of 1.5 kg for 1 kg of fiberglass mat). So materials alone multiply the base price of furniture by 233.
The shelf mass reduction lead to a 68 % gain. Now, if we reverse-engineer the mass of this camping-van :
| Object | Mass (kg) | Gasoline consumption (L/100km) |
| Empty Citroen Jumper L3H2 160 HP Blue HDi | 2050 | 8.4 |
| Fully loaded Citroen Jumper L3H2 160 HP Blue HDi | 3500 | 11 |
| Pössl 2 Win plus in riding condition with 20 L water in the tanks | 2840 | 9.9* |
| Whole equipment (without water) | 770 | |
| Gaz tank | 26 | |
| Boiler/heater | 15 | |
| Bed | 35* | |
| Battery | 25 | |
| Water tanks (empty) | 10 ? | |
| Fridge | 20 | |
| Toilet | 10 | |
| Furniture / Piping / others | 600* | |
| Target equipement mass reduction | - 390 | |
| Optimized Pössl 2 Win on Citroen Jumper L3H2 110 HP Blue HDi | 2430 | 9* |
If you assume an overall mass reduction of 65 % over the furniture, that’s 415 kg less, then 0.9 L/100 km of gasoline saving, so by today’s price, around 1.40 €/100 km saved. But… with such a reduced mass, one could definitely switch to a lighter van to save on the vehicle too : the citroen Jumper 110 HP 3300 kg version is 5650 € cheaper and you still get 850 kg of headroom before the load limit (more than the Pössl version that has only 660 kg). That’s more than enough for two 70 kg persons even including 190 L of water in the tanks. That makes you save on the tires and the brakes too.
We built a full electric car driving at 110 km/h top and protecting the driver up to a 6 G impact that weighted less than 300 kg including 25 kg motors and 50 kg Li-Po batteries. A van already has a shell we can use to take some of the load, so a 220 kg inside structure primarily designed to hold your coats and food supplies is still conservative and leave some space to improvement.
The camping van shown above costs 51 800 €, the base price of the bare cargo Citroen Jumper van is 42 235 €, so the equiped furniture and work is worth 9565 €. Considering the whole surface of panels in that van (estimated to 44 m², because the volume of chipwood is estimated to 0.8 m³ = 600 kg / 750 kg/m³), the material price increases from 4 € to 933 €. As for the additional cost of manufacturing, again, I have no clue. I roughly evaluate it as 8 times as much time, because of the curing delay, but parallelized between several vans… It could be less.
So, overall, the total mass reduction cost alone would be absorbed in gas savings after 67 000 km, assuming the same van is used, which is a few years of intensive use. But, if you consider that you could undersize the van motor and chassis as well, you probably saved more than 4000 € already before the first kilometer with a lighter design. Moreover, a lighter design goes easier on the tires and dampers, so some savings are to expect there too.
So, after all, this is economically sustainable only if we plan on gas becoming way more expensive, with a van used intensively. For a recreative occasional use, it is not worth it, and it is a heartbreak to see that wasting energy is still more profitable than trying to do good. For the new nomads (“vanlifers”) who live full-time on the road, that might be worth considerating though, if not for today, at least as an investment.